Tutorial
tutorial.RmdExample 1: Returns to Office of China’s NPC
We illustrate tjbal using a dataset from Truex (2014), in which the author investigates the returns to seats in China’s National People’s Congress by CEOs of listed firms. The dataset npc is shipped with the tjbal package (we dropped one treated firm with extremely large revenue in 2007 to improve overlap between the treated and control units; see details in the paper). To load the package and the dataset:
library(tjbal)
#> ## Syntax has changed since v.0.4.0.
#> ## See http://bit.ly/tjbal4r for more info.
#> ## Comments and suggestions -> yiqingxu@stanford.edu.
data(tjbal)
ls()
#> [1] "germany" "npc"
head(npc)
#> gvkey fyear roa treat so_portion rev2007
#> 1 108893 2005 0.13556981 0 0.5286272 15110.46
#> 2 108893 2006 0.10115566 0 0.5286272 15110.46
#> 3 108893 2007 0.12335894 0 0.5286272 15110.46
#> 4 108893 2008 0.20065501 1 0.5286272 15110.46
#> 5 108893 2009 0.06594828 1 0.5286272 15110.46
#> 6 108893 2010 0.12756890 1 0.5286272 15110.46First, we take a look at the data structure. The outcome variable is
roa and the treatment indicator is treat; the
unit and time indicators are gvkey and fyear,
respectively. There are 47 treated firms whose CEOs became NPC members
in 2008 and 939 control firms whose CEOs were never NPC members from
2005 to 2010.
The following plot shows the treatment status of the first 50 firms based on firm ID:
library(panelView)
#> ## See bit.ly/panelview4r for more info.
#> ## Report bugs -> yiqingxu@stanford.edu.
panelview(roa ~ treat + so_portion + rev2007, data = npc, show.id = c(1:50),
index = c("gvkey","fyear"), xlab = "Year", ylab = "Firm ID",
axis.lab.gap = c(0,1), by.timing = TRUE,
display.all = TRUE, axis.lab = "time")
#> If the number of units is more than 300, we set "gridOff = TRUE".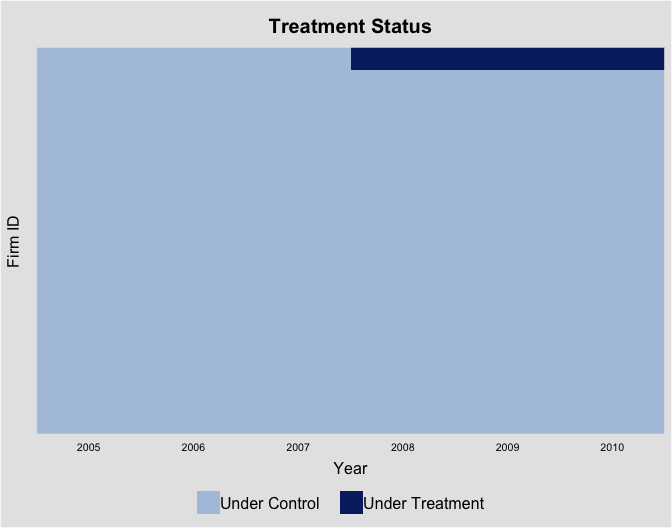
with(npc, table(fyear, treat))
#> treat
#> fyear 0 1
#> 2005 986 0
#> 2006 986 0
#> 2007 986 0
#> 2008 939 47
#> 2009 939 47
#> 2010 939 47Difference-in-Differences (DID)
We then apply the difference-in-differences (DiD) method without
controlling for any covariates. In the formula of
tjbal, the left-hand-side variable is the outcome and
the first right-hand-side variable is the dichotomous treatment
indicator. We specify unit and time indicators using the
index option. At the moment, we do not want to balance on
pre-treatment outcomes, therefore, we set Y.match.npre = 0.
Because an DID approach involves subtracting pre-treatment means from
the outcome for each unit, we set demean = TRUE.
Uncertainty estimates are obtained via a bootstrap procedure.
tjbal provides three balancing approaches: (1)
"mean", which stands for mean-balancing; (2)
"kernel", which stands for kernel-balancing; and (3)
"meanfirst", which stands for kernel balancing with mean
balancing constraints. "meanfirst" will prioritize
balancing on covariate means over higher-order terms and interactions.
The default option is "meanfirst". In this case, because we
do not have any covariates to seek balance on, the
estimator option is redundant.
For datasets with only one treatment timing, tjbal
provides three types of uncertainty estimates:
vce = "fixed.weights" which treats balancing weights as
fixed; "jackknife" (or "jack"), which conducts
jackknife by omitting one treated unit at a time, and
"bootstrap" (or "boot"), which conducts
non-parametric bootstrapping by reshuffle both the treated and control
units. We show in the paper that, with reasonably large samples, these
three methods yield very similar results. When "jackknife"
or "bootstrap" is chosen, nsims determines the
number of jackknife or bootstrap runs. With jackknife,
nsims will be ignored if it is bigger than the number of
treated units.
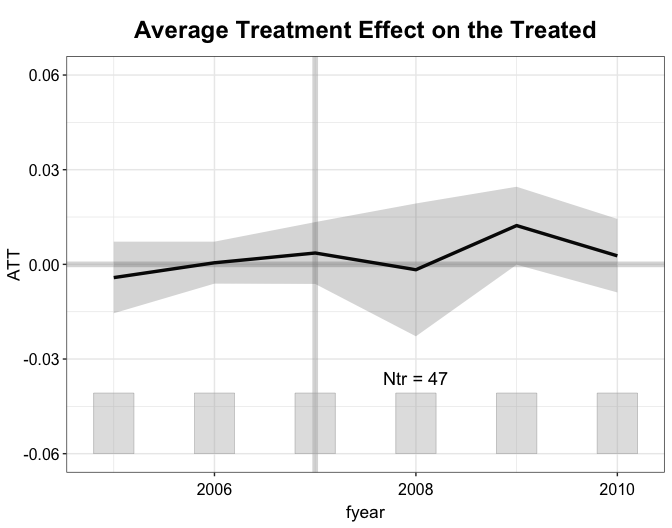
The print function present the result, which shows a non-significant effect of NPC membership on firms’ return on assets (ROA).
out.did <- tjbal(roa ~ treat, data = npc,
index = c("gvkey","fyear"), Y.match.npre = 0,
demean = TRUE, vce = "boot", nsims = 200)
#>
#> Bootstrapping...
#> Parallel computing...
print(out.did)
#> Call:
#> tjbal.formula(formula = roa ~ treat, data = npc, index = c("gvkey",
#> "fyear"), Y.match.npre = 0, demean = TRUE, vce = "boot",
#> nsims = 200)
#>
#> ~ by Period (including Pre-treatment Periods):
#> ATT S.E. z-score CI.lower CI.upper p.value n.Treated
#> 2005 -0.0042 0.0061 -0.6851 -0.0160 0.0077 0.4933 47
#> 2006 0.0005 0.0038 0.1428 -0.0069 0.0080 0.8865 47
#> 2007 0.0036 0.0047 0.7620 -0.0057 0.0129 0.4461 47
#> 2008 -0.0017 0.0106 -0.1644 -0.0225 0.0190 0.8694 47
#> 2009 0.0123 0.0068 1.8186 -0.0010 0.0255 0.0690 47
#> 2010 0.0027 0.0062 0.4437 -0.0094 0.0149 0.6573 47
#>
#> Average Treatment Effect on the Treated:
#> ATT S.E. z-score CI.lower CI.upper p.value
#> [1,] 0.0044 0.0063 0.706 -0.0079 0.0167 0.4802The plot function visualizes the result, By default
(type = gap), it plots the average treatment effect on the
treated (ATT) over time (from 2008 to 2010). We add a histogram to
illustrate the number of treated units at the bottom of the figure. It
can be turned off by setting count == FALSE.
We can also plot the treated and estimated \(Y(0)\) averages by specifying
type = "counterfactual or simply type = "ct".
Note that, with the DID approach, the estimated \(Y(0)\) averages do not fit perfectly with
the treated averaged over the pre-treatment periods.
plot(out.did, type = "counterfactual", count = FALSE)
The plot function can also visualize the distribution of weights of the control units (the total weights added up to \(N_{tr}\), the number of the treated units). With the DID method, all control units are equally weighted:
plot(out.did, type = "weights")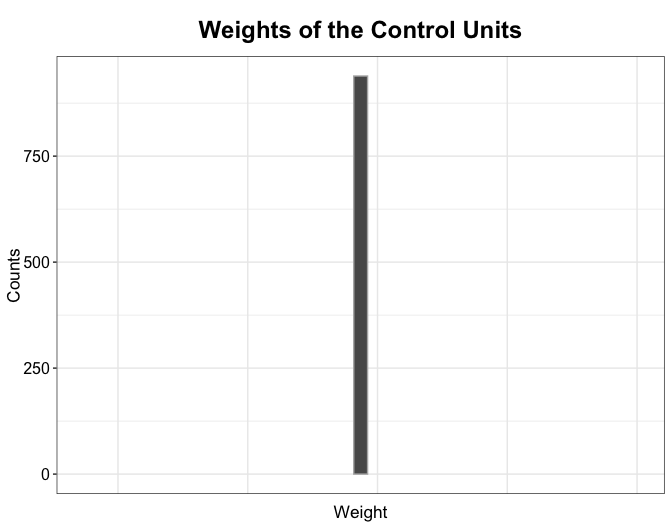
Mean Balancing
Next, we apply the mean balancing approach (which the author uses in
the original paper). In the formula, we also add two covariates,
so_portion and rev2007. Note that they will
not be put into regressions directly; rather, the algorithm will seek
balance on them as well as the three pre-treatment outcomes. Because we
do not employ the kernel transformation, we set
estimator = "mean".
out.mbal <- tjbal(roa ~ treat + so_portion + rev2007, data = npc,
index = c("gvkey","fyear"), demean = FALSE, estimator = "mean",
vce = "jackknife")
#> Seek balance on:
#> roa2005, roa2006, roa2007, so_portion, rev2007
#>
#> Optimization:
#> bias.ratio = 0.0000; num.dims = 5 (mbal)
#>
#> Balance Table
#> mean.tr mean.co.pre mean.co.pst sd.tr sd.co.pre sd.co.pst
#> roa2005 0.0376 0.0225 0.0376 0.0675 0.0801 0.0778
#> roa2006 0.0503 0.0305 0.0503 0.0424 0.0756 0.0667
#> roa2007 0.0643 0.0414 0.0643 0.0564 0.1035 0.1611
#> so_portion 0.3170 0.2491 0.3170 0.2397 0.2218 0.2355
#> rev2007 6420.3705 2647.3412 6420.3705 9547.6633 5530.8308 14355.1192
#> diff.pre diff.pst
#> roa2005 0.2243 0
#> roa2006 0.4682 0
#> roa2007 0.4062 0
#> so_portion 0.2835 0
#> rev2007 0.3952 0
#>
#> Jackknife...
#> Parallel computing...We see that NPC membership increases ROA by about 2 percentage points, and it is highly statistically significant.
print(out.mbal)
#> Call:
#> tjbal.formula(formula = roa ~ treat + so_portion + rev2007, data = npc,
#> index = c("gvkey", "fyear"), demean = FALSE, estimator = "mean",
#> vce = "jackknife")
#>
#> ~ by Period (including Pre-treatment Periods):
#> ATT S.E. z-score CI.lower CI.upper p.value n.Treated
#> 2005 0.0000 0.0000 0.0001 0.0000 0.0000 0.9999 47
#> 2006 0.0000 0.0000 -0.0038 0.0000 0.0000 0.9969 47
#> 2007 0.0000 0.0000 -0.0054 0.0000 0.0000 0.9957 47
#> 2008 0.0161 0.0076 2.1216 0.0012 0.0310 0.0339 47
#> 2009 0.0260 0.0057 4.5312 0.0147 0.0372 0.0000 47
#> 2010 0.0203 0.0064 3.1939 0.0079 0.0328 0.0014 47
#>
#> Average Treatment Effect on the Treated:
#> ATT S.E. z-score CI.lower CI.upper p.value
#> [1,] 0.0208 0.0057 3.628 0.0096 0.032 3e-04Alternatively, we can also specify the outcome (Y),
treatment (D), and covariates (X)
separately.
out.mbal <- tjbal(data = npc, Y = "roa", D = "treat", X = c("so_portion","rev2007"),
index = c("gvkey","fyear"), demean = FALSE, estimator = "mean",
vce = "jackknife", nsims = 200)We show the gap plot, the counterfactual
plot, and the weightsplot again. With mean balancing, the
pre-treatment outcomes are perfectly balanced between the treatment and
control groups.
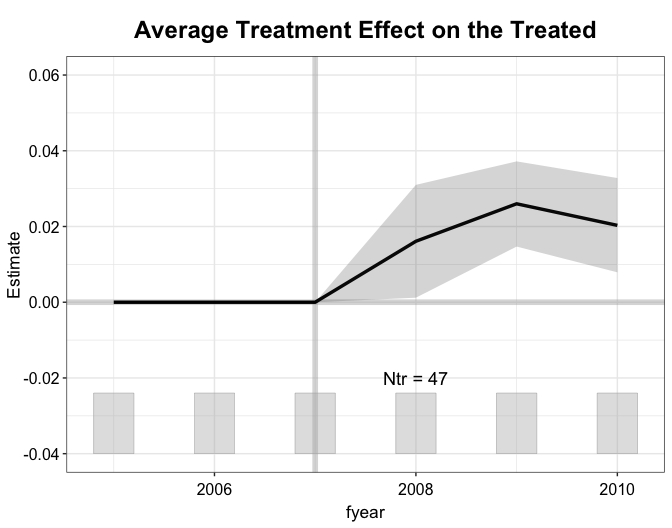
plot(out.mbal, type = "ct")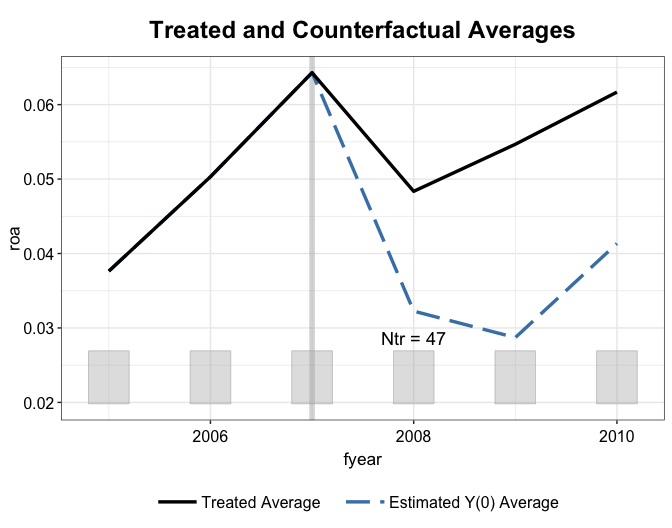
We can also add two bands that represent the ranges of the 5 to 95%
quantile of the treated and control trajectories to the plot by setting
raw = "band". When trim = TRUE (default), the
control group data will be trimmed based on weights assigned to the
control units (up to 90% of the total weight).
We can change the font size of almost all elements in the figure by
setting cex.main (for title), cex.lab (for
axis titles), cex.axis (for numbers on the axes),
cex.legend (for legend) and cex.text for text
in the figure. The numbers are all relative to the default.
A set of legend options can be used to adjust the look of the
legends, including legendOff (turn off legends),
legend.pos (position), legend.ncol (number of
columns), and legend.labs (change label texts).
plot(out.mbal, type = "ct", raw = "band", ylim = c(-0.2, 0.3),
cex.main = 0.9, cex.lab = 1.1, cex.axis = 0.9, cex.legend= 0.8, cex.text = 1.5,
legend.pos = "top")
plot(out.mbal, type = "weights")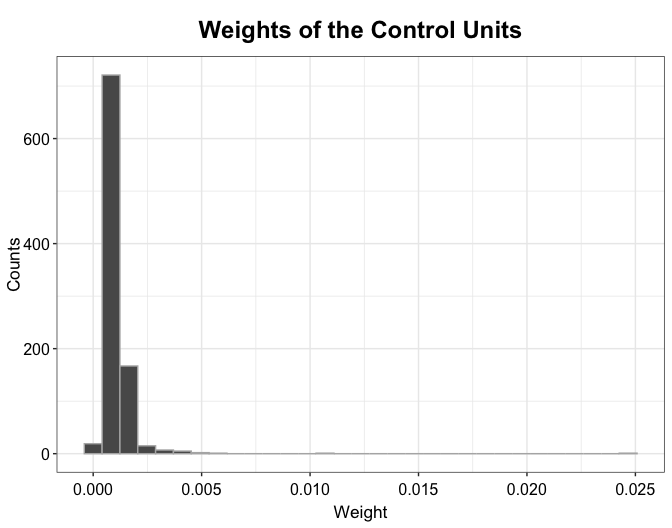
The plot function can also check balance in pre-treatment outcomes and covariates between the treatment and control groups before and after reweighting:
plot(out.mbal, type = "balance")
Kernel Balancing (w/ mean balancing constraints)
Finally, we apply the kernel balancing method (while respecting
mean-balancing constraints) by setting
estimator = "meanfirst". Note that kernel balancing is
significantly more computationally intensive than mean balancing.
Parallel computing with 4 cores on a 2016 iMac takes about 1 minutes to
finish 47 jackknife runs.
begin.time<-Sys.time()
out.kbal <- tjbal(roa ~ treat + so_portion + rev2007, data = npc,
index = c("gvkey","fyear"), estimator = "meanfirst", demean = FALSE, vce = "jackknife")
#> Seek balance on:
#> roa2005, roa2006, roa2007, so_portion, rev2007
#>
#> Optimization:
#> bias.ratio = 0.0950; num.dims = 5 + 43 (mbal + kbal)
#>
#> Balance Table
#> mean.tr mean.co.pre mean.co.pst sd.tr sd.co.pre sd.co.pst
#> roa2005 0.0376 0.0225 0.0376 0.0675 0.0801 0.0658
#> roa2006 0.0503 0.0305 0.0503 0.0424 0.0756 0.0425
#> roa2007 0.0643 0.0414 0.0643 0.0564 0.1035 0.0541
#> so_portion 0.3170 0.2491 0.3170 0.2397 0.2218 0.2378
#> rev2007 6420.3705 2647.3412 6420.3704 9547.6633 5530.8308 9410.3702
#> diff.pre diff.pst
#> roa2005 0.2243 0
#> roa2006 0.4682 0
#> roa2007 0.4062 0
#> so_portion 0.2835 0
#> rev2007 0.3952 0
#>
#> Jackknife...
#> Parallel computing...
print(Sys.time()-begin.time)
#> Time difference of 1.50954 minsWith kernel balancing with mean balancing weights, we find that NPC membership of the CEO increases a firm’s ROA by 1.4 percentage points. The estimate remains highly statistically significant.
print(out.kbal)
#> Call:
#> tjbal.formula(formula = roa ~ treat + so_portion + rev2007, data = npc,
#> index = c("gvkey", "fyear"), demean = FALSE, estimator = "meanfirst",
#> vce = "jackknife")
#>
#> ~ by Period (including Pre-treatment Periods):
#> ATT S.E. z-score CI.lower CI.upper p.value n.Treated
#> 2005 0.0000 0.0011 0.0000 -0.0021 0.0021 1.0000 47
#> 2006 0.0000 0.0010 0.0000 -0.0020 0.0020 1.0000 47
#> 2007 0.0000 0.0008 0.0000 -0.0016 0.0016 1.0000 47
#> 2008 0.0045 0.0080 0.5665 -0.0112 0.0202 0.5711 47
#> 2009 0.0194 0.0095 2.0469 0.0008 0.0380 0.0407 47
#> 2010 0.0140 0.0092 1.5231 -0.0040 0.0321 0.1277 47
#>
#> Average Treatment Effect on the Treated:
#> ATT S.E. z-score CI.lower CI.upper p.value
#> [1,] 0.0127 0.0068 1.851 -7e-04 0.0261 0.0642Balance (in means) in the pre-treatment outcomes and covariates remain great, but no longer perfect. This is because kernel balancing also attempts to achieve balance in high-order features of these variables.
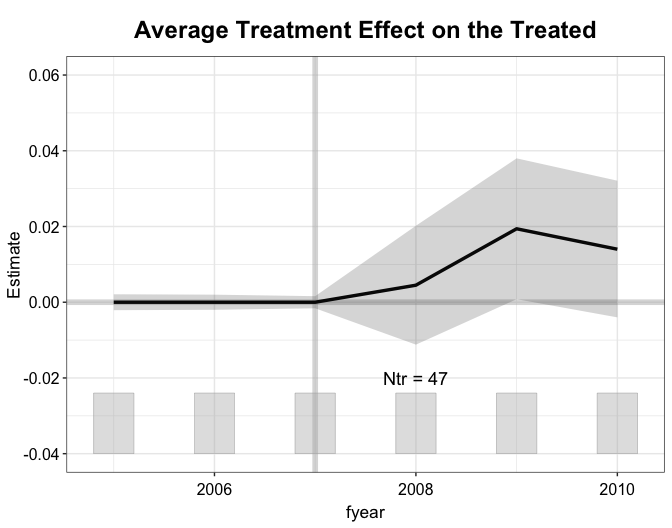
plot(out.kbal, type = "ct", xlab = "Year", ylab = "Return to Assets")
plot(out.kbal, type = "weights")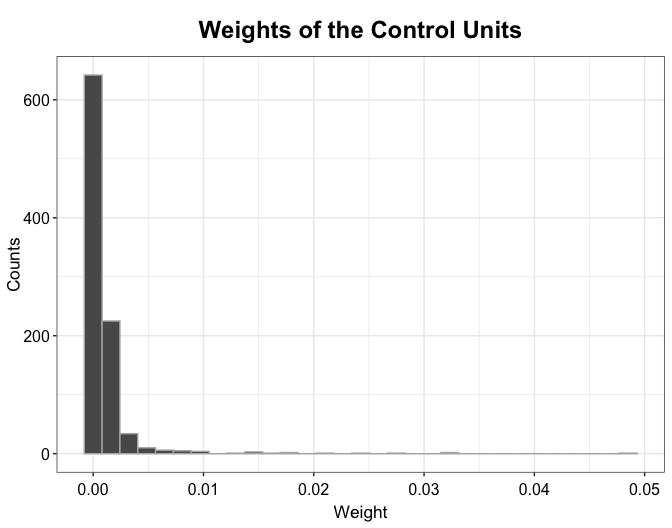
plot(out.kbal, type = "balance")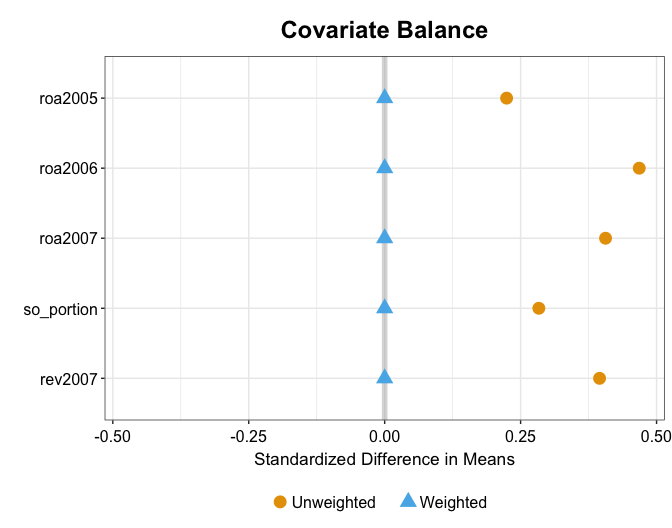
For example, kernel balancing also makes the standard deviations (or variance) of these variables in the treatment and reweighted control groups more similar than mean balancing.
plot(out.mbal, type = "balance", stat = "sd")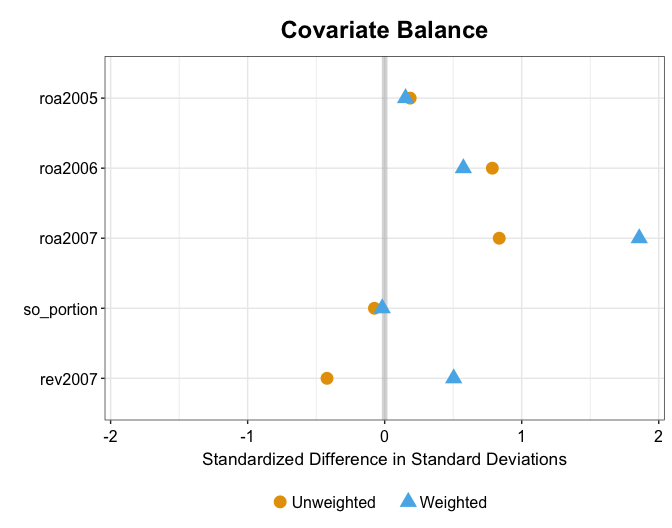
plot(out.kbal, type = "balance", stat = "sd")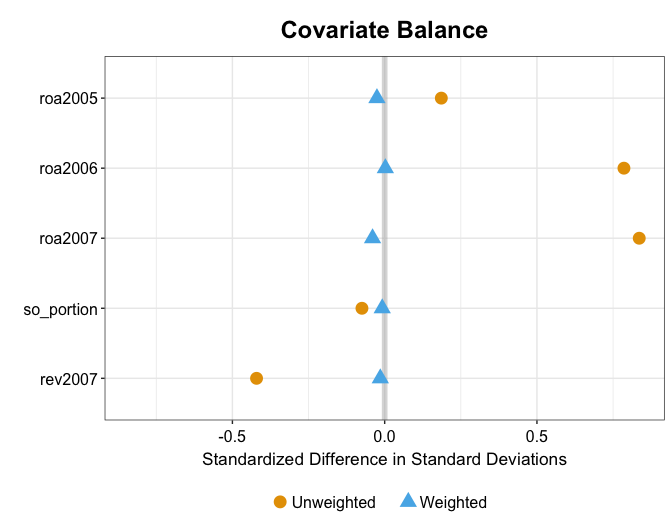
For this example, setting estimator = "kernel"
(i.e. kernel balancing without incorporating mean balancing constraints)
yields very similar results.
Example 2: German Reunification
In the second example, we re-investigate the effect of German
reunification on West Germany’s GDP growth using data from Abadie, Diamond, and Hainmueller (2015).
Variable treat indicate West Germany over the post-1990
periods. Again, we look at the data structure first:
panelview(data = germany, gdp ~ treat, index = c("country","year"),
xlab = "Year", ylab = "Country", by.timing = TRUE,
axis.adjust = TRUE, axis.lab.gap = c(1,0))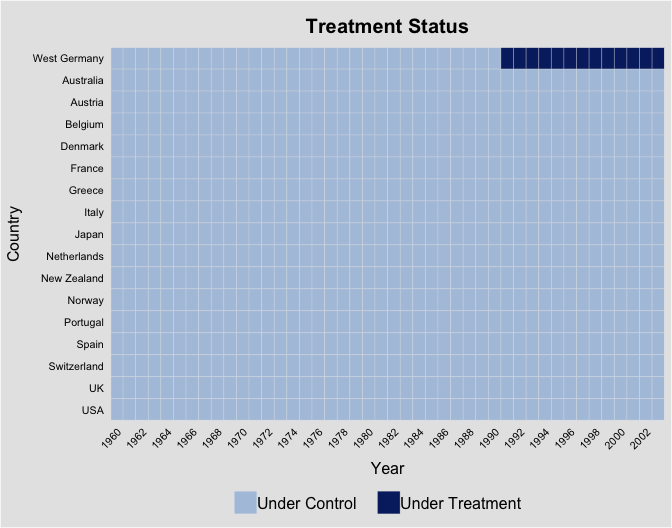
Next, we implement the mean balancing method. Different from the
previous example, we take averages for the covariates over different
time periods (to be consistent with the original paper). Make sure that
the length of the list set by X.avg.time is the the same as
the length of the variable names in X.
out2.mbal <- tjbal(data = germany, Y = "gdp", D = "treat", Y.match.time = c(1960:1990),
X = c("trade","infrate","industry", "schooling", "invest80"),
X.avg.time = list(c(1981:1990),c(1981:1990),c(1981:1990),c(1980:1985),c(1980)),
index = c("country","year"), demean = TRUE)
#> Too few treated unit(s). Uncertainty estimates not provided.
#> Seek balance on:
#> gdp.dm1960, gdp.dm1961, gdp.dm1962, gdp.dm1963, gdp.dm1964, gdp.dm1965, gdp.dm1966, gdp.dm1967, gdp.dm1968, gdp.dm1969, gdp.dm1970, gdp.dm1971, gdp.dm1972, gdp.dm1973, gdp.dm1974, gdp.dm1975, gdp.dm1976, gdp.dm1977, gdp.dm1978, gdp.dm1979, gdp.dm1980, gdp.dm1981, gdp.dm1982, gdp.dm1983, gdp.dm1984, gdp.dm1985, gdp.dm1986, gdp.dm1987, gdp.dm1988, gdp.dm1989, gdp.dm1990, trade, infrate, industry, schooling, invest80
#>
#> Optimization:
#> bias.ratio = 0.5468; num.dims = 2 + 0 (mbal + kbal)
#>
#> Balance Table
#> mean.tr mean.co.pre mean.co.pst diff.pre diff.pst
#> gdp.dm1960 -6282.4516 -5549.6673 -6575.8498 -0.1166 0.0467
#> gdp.dm1961 -6178.4516 -5438.3548 -6465.1921 -0.1198 0.0464
#> gdp.dm1962 -6039.4516 -5319.6673 -6313.2363 -0.1192 0.0453
#> gdp.dm1963 -5956.4516 -5207.3548 -6194.2952 -0.1258 0.0399
#> gdp.dm1964 -5760.4516 -5053.4798 -6005.0548 -0.1227 0.0425
#> gdp.dm1965 -5561.4516 -4901.0423 -5815.6146 -0.1187 0.0457
#> gdp.dm1966 -5398.4516 -4711.6673 -5589.3747 -0.1272 0.0354
#> gdp.dm1967 -5325.4516 -4556.1048 -5402.9393 -0.1445 0.0146
#> gdp.dm1968 -4995.4516 -4292.0423 -5090.7819 -0.1408 0.0191
#> gdp.dm1969 -4568.4516 -3937.3548 -4693.9368 -0.1381 0.0275
#> gdp.dm1970 -4199.4516 -3600.3548 -4292.2593 -0.1427 0.0221
#> gdp.dm1971 -3880.4516 -3286.1673 -3901.6583 -0.1531 0.0055
#> gdp.dm1972 -3511.4516 -2929.7298 -3485.5438 -0.1657 -0.0074
#> gdp.dm1973 -3013.4516 -2434.9798 -2934.4072 -0.1920 -0.0262
#> gdp.dm1974 -2492.4516 -1929.8548 -2332.1177 -0.2257 -0.0643
#> gdp.dm1975 -1963.4516 -1482.7923 -1892.0915 -0.2448 -0.0363
#> gdp.dm1976 -1199.4516 -921.0423 -1251.1953 -0.2321 0.0431
#> gdp.dm1977 -476.4516 -381.5423 -520.8741 -0.1992 0.0932
#> gdp.dm1978 361.5484 289.7702 301.2427 0.1985 0.1668
#> gdp.dm1979 1500.5484 1157.7702 1341.5094 0.2284 0.1060
#> gdp.dm1980 2516.5484 2083.5202 2452.4602 0.1721 0.0255
#> gdp.dm1981 3548.5484 3020.6452 3629.7422 0.1488 -0.0229
#> gdp.dm1982 4194.5484 3664.8327 4228.9958 0.1263 -0.0082
#> gdp.dm1983 4952.5484 4284.3327 5018.3650 0.1349 -0.0133
#> gdp.dm1984 5914.5484 5052.1452 6089.4276 0.1458 -0.0296
#> gdp.dm1985 6724.5484 5795.8327 7014.5704 0.1381 -0.0431
#> gdp.dm1986 7431.5484 6408.8952 7721.2870 0.1376 -0.0390
#> gdp.dm1987 8112.5484 7075.5202 8463.7659 0.1278 -0.0433
#> gdp.dm1988 9219.5484 8033.7702 9592.0343 0.1286 -0.0404
#> gdp.dm1989 10427.5484 9064.5827 10870.3999 0.1307 -0.0425
#> gdp.dm1990 11898.5484 10001.5827 12032.6221 0.1594 -0.0113
#> trade 56.7778 59.8313 59.1378 -0.0538 -0.0416
#> infrate 2.5948 7.6166 4.6865 -1.9353 -0.8061
#> industry 34.5385 33.7944 32.1820 0.0215 0.0682
#> schooling 55.5000 38.6594 50.8456 0.3034 0.0839
#> invest80 27.0180 25.8952 25.5263 0.0416 0.0552Alternatively, we can use the following syntax:
out2.kbal <- tjbal(gdp ~ treat + trade + infrate + industry + schooling + invest80,
data = germany, Y.match.time = c(1960:1990), X.avg.time = list(c(1981:1990), c(1981:1990), c(1981:1990),c(1980:1985),c(1980)),
index = c("country","year"), estimator = "kernel", demean = TRUE)
#> Too few treated unit(s). Uncertainty estimates not provided.
#> Seek balance on:
#> gdp.dm1960, gdp.dm1961, gdp.dm1962, gdp.dm1963, gdp.dm1964, gdp.dm1965, gdp.dm1966, gdp.dm1967, gdp.dm1968, gdp.dm1969, gdp.dm1970, gdp.dm1971, gdp.dm1972, gdp.dm1973, gdp.dm1974, gdp.dm1975, gdp.dm1976, gdp.dm1977, gdp.dm1978, gdp.dm1979, gdp.dm1980, gdp.dm1981, gdp.dm1982, gdp.dm1983, gdp.dm1984, gdp.dm1985, gdp.dm1986, gdp.dm1987, gdp.dm1988, gdp.dm1989, gdp.dm1990, trade, infrate, industry, schooling, invest80
#>
#> Optimization:
#> bias.ratio = 0.8091; num.dims = 1 (kbal)
#>
#> Balance Table
#> mean.tr mean.co.pre mean.co.pst diff.pre diff.pst
#> gdp.dm1960 -6282.4516 -5549.6673 -5795.5598 -0.1166 -0.0775
#> gdp.dm1961 -6178.4516 -5438.3548 -5705.1750 -0.1198 -0.0766
#> gdp.dm1962 -6039.4516 -5319.6673 -5568.4468 -0.1192 -0.0780
#> gdp.dm1963 -5956.4516 -5207.3548 -5457.5674 -0.1258 -0.0838
#> gdp.dm1964 -5760.4516 -5053.4798 -5300.1505 -0.1227 -0.0799
#> gdp.dm1965 -5561.4516 -4901.0423 -5160.3940 -0.1187 -0.0721
#> gdp.dm1966 -5398.4516 -4711.6673 -4961.5077 -0.1272 -0.0809
#> gdp.dm1967 -5325.4516 -4556.1048 -4780.8164 -0.1445 -0.1023
#> gdp.dm1968 -4995.4516 -4292.0423 -4498.4115 -0.1408 -0.0995
#> gdp.dm1969 -4568.4516 -3937.3548 -4129.7337 -0.1381 -0.0960
#> gdp.dm1970 -4199.4516 -3600.3548 -3786.3056 -0.1427 -0.0984
#> gdp.dm1971 -3880.4516 -3286.1673 -3487.6178 -0.1531 -0.1012
#> gdp.dm1972 -3511.4516 -2929.7298 -3145.7532 -0.1657 -0.1041
#> gdp.dm1973 -3013.4516 -2434.9798 -2653.5151 -0.1920 -0.1194
#> gdp.dm1974 -2492.4516 -1929.8548 -2097.7868 -0.2257 -0.1583
#> gdp.dm1975 -1963.4516 -1482.7923 -1599.2937 -0.2448 -0.1855
#> gdp.dm1976 -1199.4516 -921.0423 -985.3133 -0.2321 -0.1785
#> gdp.dm1977 -476.4516 -381.5423 -428.6132 -0.1992 -0.1004
#> gdp.dm1978 361.5484 289.7702 275.6705 0.1985 0.2375
#> gdp.dm1979 1500.5484 1157.7702 1229.2199 0.2284 0.1808
#> gdp.dm1980 2516.5484 2083.5202 2216.4550 0.1721 0.1192
#> gdp.dm1981 3548.5484 3020.6452 3212.5685 0.1488 0.0947
#> gdp.dm1982 4194.5484 3664.8327 3897.7849 0.1263 0.0707
#> gdp.dm1983 4952.5484 4284.3327 4578.8684 0.1349 0.0755
#> gdp.dm1984 5914.5484 5052.1452 5349.6508 0.1458 0.0955
#> gdp.dm1985 6724.5484 5795.8327 6129.5811 0.1381 0.0885
#> gdp.dm1986 7431.5484 6408.8952 6766.7423 0.1376 0.0895
#> gdp.dm1987 8112.5484 7075.5202 7479.4055 0.1278 0.0780
#> gdp.dm1988 9219.5484 8033.7702 8476.1354 0.1286 0.0806
#> gdp.dm1989 10427.5484 9064.5827 9496.5271 0.1307 0.0893
#> gdp.dm1990 11898.5484 10001.5827 10433.3520 0.1594 0.1231
#> trade 56.7778 59.8313 59.2553 -0.0538 -0.0436
#> infrate 2.5948 7.6166 6.3965 -1.9353 -1.4651
#> industry 34.5385 33.7944 33.8506 0.0215 0.0199
#> schooling 55.5000 38.6594 41.2716 0.3034 0.2564
#> invest80 27.0180 25.8952 26.4878 0.0416 0.0196We plot the estimated treatment effect from both mean balancing and kernel balancing. It seems that the kernel balancing approach yield slightly better pre-treatment fit—this is not always the case.
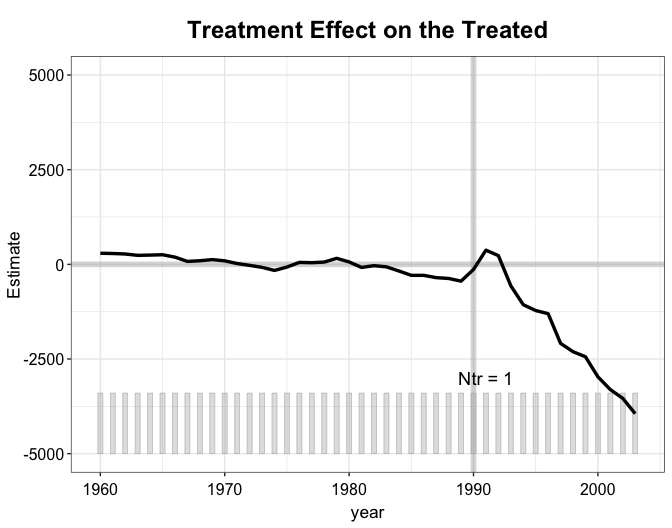

The estimated counterfactual for West Germany.
plot(out2.mbal, type = "counterfactual", count = FALSE) 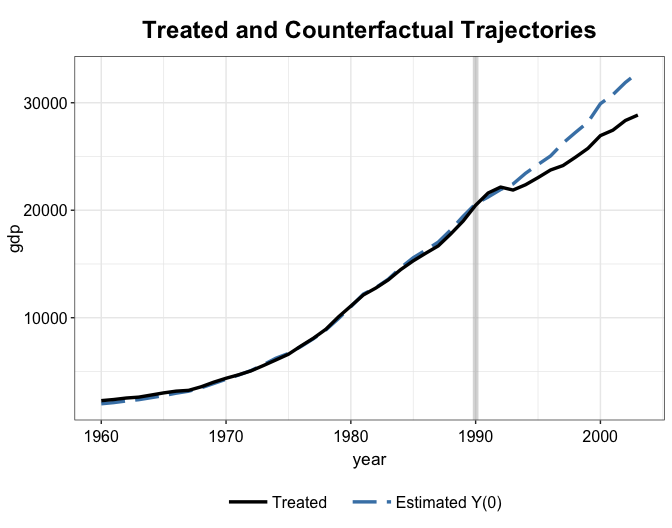
plot(out2.kbal, type = "ct", count = FALSE) 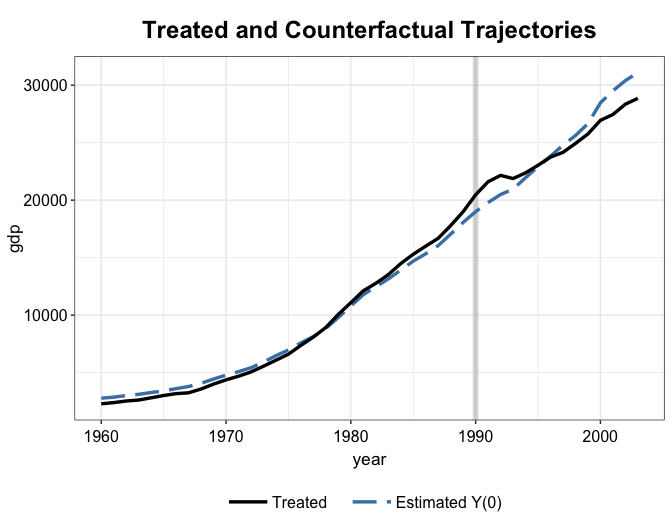
By setting raw = "all" and trim = TRUE
(default), we can add to the counterfactual plot the trajectories of the
heavily weighted control units, whose assigned weights add up to 90% of
the total weight. The number 90% can be adjusted by the
trim.wtot option. If trim = FALSE, all control
trajectories will be shown.
plot(out2.mbal, type = "ct", raw = "all", trim.wtot = 0.9) 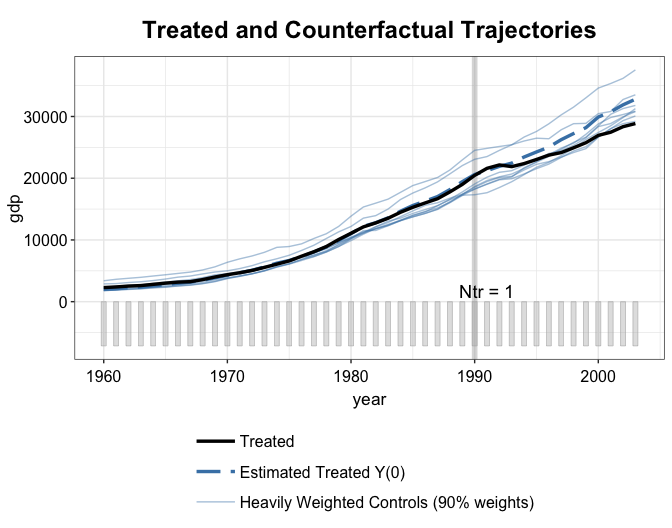
We can see that kernel balancing put more weights on a much smaller number of control units.
plot(out2.kbal, type = "ct", raw = "all") 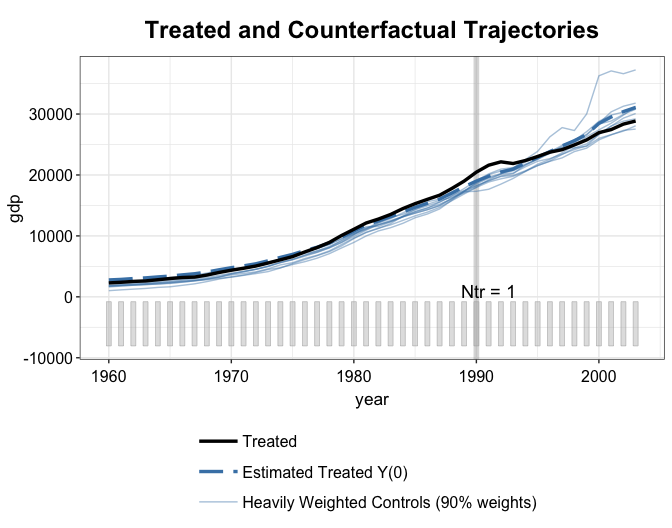
By setting raw = "band" and trim = "TRUE"
(default), we show the range of the trajectories of heavily weighted
controls.
plot(out2.mbal, type = "ct", raw = "band") 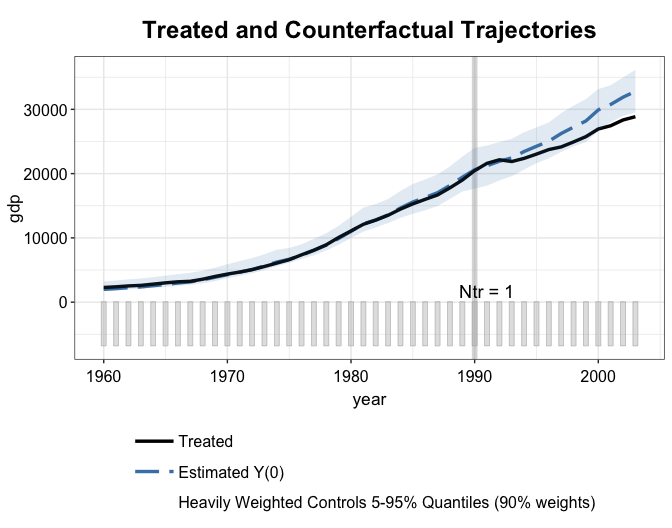
Finally, the weights plot confirms that kernel balancing
puts more weights on fewer control units.
plot(out2.mbal, type = "weights")
plot(out2.kbal, type = "weights")