3  Gsynth Program

In this chapter, we demonstrate how to use the fect package to implement the generalized synthetic control method (Gsynth), which was originally implemented by the gsynth package (all functionalities are transferred now). Gsynth (method = "gsynth") and FEct/IFEct/MC (method = "fe"/"ife"/"mc") are different in the following ways:

• Gsynth is designed to handle block and staggered DID settings without treatment reversal, whereas other methods allow for treatment reversal under the assumption of limited carryover effects.
• Gsynth is particularly suited for cases where the number of treated units is small, including scenarios with only one treated unit. By setting vartype = "parametric", we can use a two-stage parametric bootstrapping procedure—analogous to conformal inference—to produce uncertainty estimates. In contrast, other methods rely on large samples, particularly a large number of treated units, to obtain reliable standard errors and confidence intervals using "bootstrap" or "jackknife".
• Compared with IFEct (method = "ife"), Gsynth does not rely on pre-treatment data from the treated units to impute \(\hat{Y}(0)\). This approach significantly speeds up computation and improves stability.

Therefore, we recommend setting method = "gsynth" in fect for scenarios where the treatment does not reverse (or is coded accordingly) and the number of treated units is small .

We will use two datasets, simgsynth and turnout, to perform analyses in block and staggered DID settings. First, we load the two datasets: simgsynth and turnout:

library(fect)
data(fect)
ls()
#> [1] "simdata"   "simgsynth" "turnout"

3.1 Simulated Data

We start with the first example, a simulated dataset described in the Xu (2017).

There are 5 treated units, 45 control units, and 30 time periods. The treatment kicks at Period 21 for all treated units, hence, a multiperiod DID set up.

head(simgsynth)
#>    id time         Y D        X1         X2 eff      error mu       alpha
#> 1 101    1  6.210998 0 0.3776736 -0.1732470   0  0.2982276  5 -0.06052364
#> 2 101    2  4.027106 0 1.7332009 -0.4945009   0  0.6365697  5 -0.06052364
#> 3 101    3  8.877187 0 1.8580159  0.4984432   0 -0.4837806  5 -0.06052364
#> 4 101    4 11.515346 0 1.3943369  1.1272713   0  0.5168620  5 -0.06052364
#> 5 101    5  5.971526 0 2.3636963 -0.1535215   0  0.3689645  5 -0.06052364
#> 6 101    6  8.237905 0 0.5370867  0.8774397   0 -0.2153805  5 -0.06052364
#>           xi          F1          L1           F2         L2
#> 1  1.1313372  0.25331851 -0.04303273  0.005764186 -0.8804667
#> 2 -1.4606401 -0.02854676 -0.04303273  0.385280401 -0.8804667
#> 3  0.7399475 -0.04287046 -0.04303273 -0.370660032 -0.8804667
#> 4  1.9091036  1.36860228 -0.04303273  0.644376549 -0.8804667
#> 5 -1.4438932 -0.22577099 -0.04303273 -0.220486562 -0.8804667
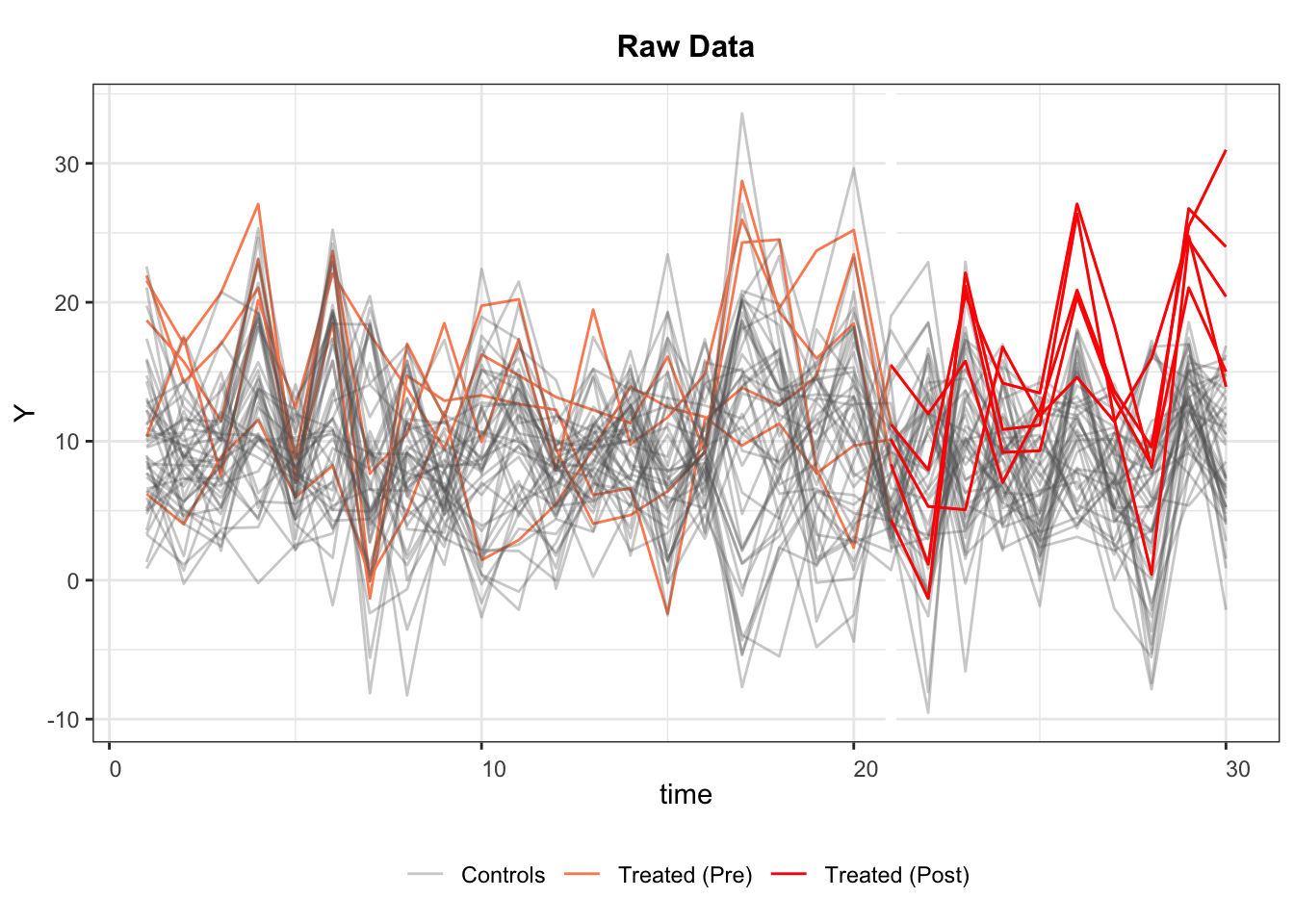
#> 6  0.7017843  1.51647060 -0.04303273  0.331781964 -0.8804667

Before we conduct any statistical analysis, it is helpful to visualize the data structure and spot missing values (if there are any). We can easily do so with the help of the panelView package. The figure below shows that: (1) there are 5 treated units and 45 control units; (2) the treated units start to be treated in period 21; and (3) there are no missing values, which is a rare case.

library(panelView)
#> ## See bit.ly/panelview4r for more info.
#> ## Report bugs -> yiqingxu@stanford.edu.
panelview(Y ~ D, data = simgsynth,  index = c("id","time"), pre.post = TRUE)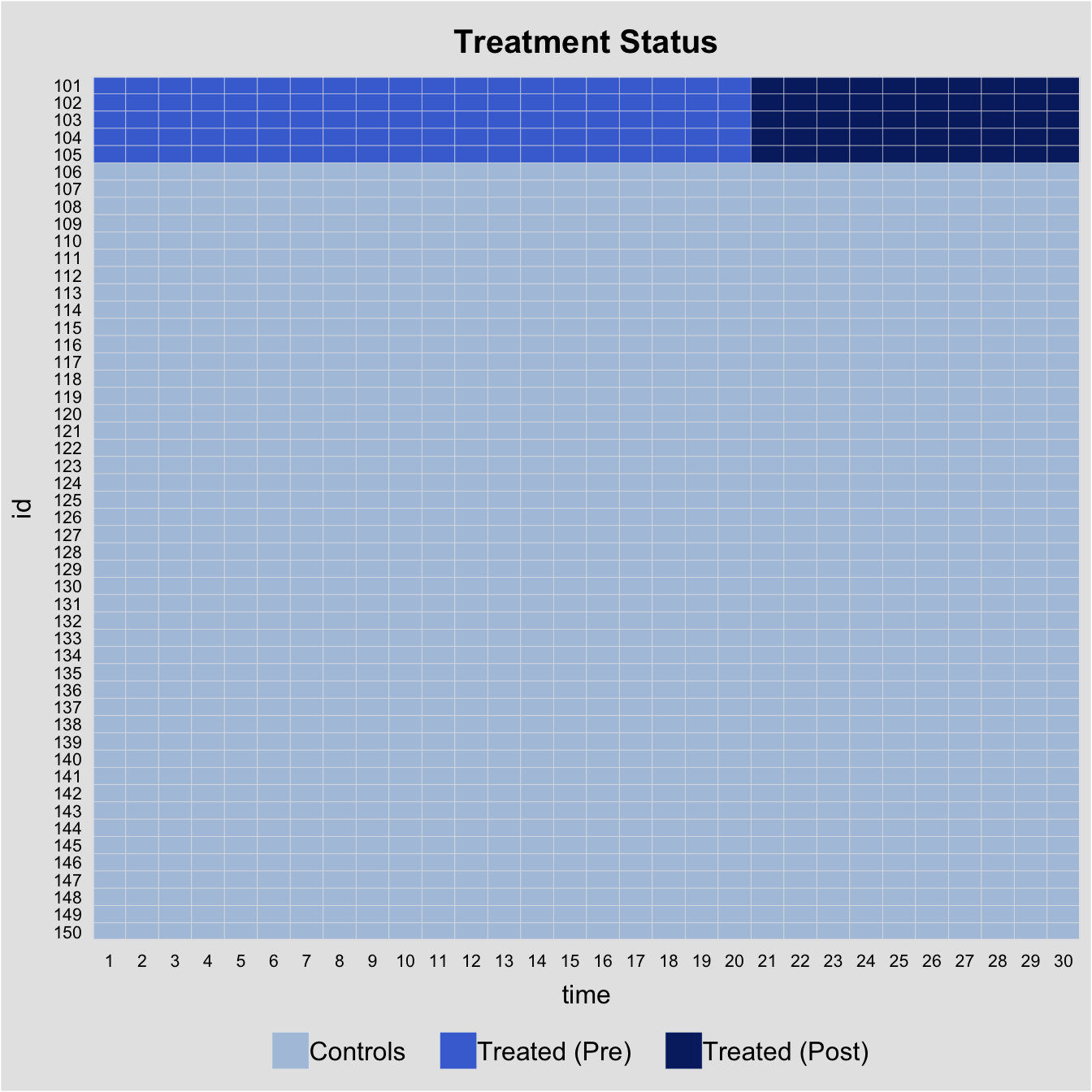 

The code chunk below visualizes the trends of outcome variable over the full panel across groups; different colors correspond to unique treatment statuses.

panelview(Y ~ D, data = simgsynth,  index = c("id","time"), type = "outcome") 

3.2 Estimation

We estimate the model using only the outcome variable (\(Y\)), treatment indicator (\(D\)), covariates (\(X_1\)) and (\(X_2\)), and group indicators (\(id\)) and (\(time\)).

To implement the Gsynth algorithm proposed in Xu (2017), set method = "gsynth".

system.time(
out <- fect(Y ~ D + X1 + X2, data = simgsynth, index = c("id","time"), 
            method = "gsynth", force = "two-way", CV = TRUE, r = c(0, 5), 
            se = TRUE, nboots = 1000, vartype = 'parametric', 
            parallel = FALSE))
#> Cross-validating ...
#> Criterion: Mean Squared Prediction Error
#> Interactive fixed effects model...
#> Cross-validating ...
#> r = 0; sigma2 = 1.84865; IC = 1.02023; PC = 1.74458; MSPE = 2.37280
#> r = 1; sigma2 = 1.51541; IC = 1.20588; PC = 1.99818; MSPE = 1.71743
#> r = 2; sigma2 = 0.99737; IC = 1.16130; PC = 1.69046; MSPE = 1.14540
#> *
#> r = 3; sigma2 = 0.94664; IC = 1.47216; PC = 1.96215; MSPE = 1.15032
#> r = 4; sigma2 = 0.89411; IC = 1.76745; PC = 2.19241; MSPE = 1.21397
#> r = 5; sigma2 = 0.85060; IC = 2.05928; PC = 2.40964; MSPE = 1.23876
#> 
#>  r* = 2
#> 
#> Bootstrapping for uncertainties ...
#> Parametric Bootstrap
#> 
Simulating errors ...
#> 1000 runs
#> Cannot use full pre-treatment periods in the F test. The first period is removed.
#>    user  system elapsed 
#>  10.392   0.141  10.701

The first variable on the right-hand side is the binary treatment indicator, with remaining variables as controls. The index option designates unit and time indicators for fixed effects analysis.

The force option (“none”, “unit”, “time”, and “two-way”) specifies the additive component(s) of the fixed effects included in the model. The default option is “two-way” (including additive unit fixed effects). A cross-validation procedure is provided (when CV = TRUE) to select the number of unobserved factors within the interval of r=c(0,5). When cross-validation is switched off, the first element in r will be set as the number of factors. Alternatively, for example, when CV = FALSE, r can take in a numeric value (r= 0).

Setting se = TRUE, the algorithm can produce uncertainty measurements. When the number of treated units is small, a parametric bootstrap procedure is preferred (vartype = "parametric"). The default number of parametric bootstrap runs is set to 200. Alternatively, non-parametric bootstrap procedure is also available. (vartype = "bootstrap"); note, it only works well when the treatment group is relatively large, (e.g. \(Ntr>40\)). The number of bootstrap runs can be set by nboots.

Because the core function of Gsynth in fect is written in C++, the algorithm runs relatively fast. The entire procedure (including cross-validation and 1,000 bootstrap runs) takes only a few seconds on a 2023 Macbook Pro Max.

The algorithm prints out the results automatically. sigma2 stands for the estimated variance of the error term; IC represents the Bayesian Information Criterion; and MPSE is the Mean Squared Prediction Error. The cross-validation procedure selects an r* that minimizes the MSPE.

Users can also use the print function to directly retrieve specific results. Here, we show three examples for the commonly requested estimates.

• est.att reports the average treatment effect on the treated (ATT) by period
• est.avg shows the ATT averaged over all periods
• est.beta represents the coefficients of the time-varying covariates

print(out)
out$est.att
out$est.avg
out$est.beta

Treatment effect estimates from each bootstrap run is stored in att.boot, an array whose dimension = (#time periods * #treated * #bootstrap runs).

The full list of generated estimates of a fect object can be found on GitHub (Line 134-239).

Parallel computing will speed up the bootstrap procedure significantly. When parallel = TRUE (default) and cores options are omitted, the algorithm will detect the number of available cores on your computer automatically.

(Warning: it may consume most of your computer’s computational power if all cores are being used.)

system.time(
out <- fect(Y ~ D + X1 + X2, data = simgsynth, index = c("id","time"), method = "gsynth", force = "two-way", CV = TRUE, r = c(0, 5), se = TRUE, nboots = 1000,vartype = 'parametric', parallel = TRUE, cores = 16)
)
#> Parallel computing ...
#> Cross-validating ...
#> Criterion: Mean Squared Prediction Error
#> Interactive fixed effects model...
#> Cross-validating ...
#> r = 0; sigma2 = 1.84865; IC = 1.02023; PC = 1.74458; MSPE = 2.37280
#> r = 1; sigma2 = 1.51541; IC = 1.20588; PC = 1.99818; MSPE = 1.71743
#> r = 2; sigma2 = 0.99737; IC = 1.16130; PC = 1.69046; MSPE = 1.14540
#> *
#> r = 3; sigma2 = 0.94664; IC = 1.47216; PC = 1.96215; MSPE = 1.15032
#> r = 4; sigma2 = 0.89411; IC = 1.76745; PC = 2.19241; MSPE = 1.21397
#> r = 5; sigma2 = 0.85060; IC = 2.05928; PC = 2.40964; MSPE = 1.23876
#> 
#>  r* = 2
#> 
#> Bootstrapping for uncertainties ...
#> Parametric Bootstrap
#> 
Simulating errors ...
#> 1000 runs
#> Cannot use full pre-treatment periods in the F test. The first period is removed.
#>    user  system elapsed 
#>   2.041   0.213   3.989

Gsynth in fect also incorporates jackknife method for uncertainty estimates.

out2 <- fect(Y ~ D + X1 + X2, data = simgsynth,  index = c("id","time"), 
               method = "gsynth", force = "two-way", 
               CV = TRUE, r = c(0, 5), se = TRUE,
               vartype = "jackknife", 
               parallel = TRUE, cores = 16)

3.3 Visualizing Results

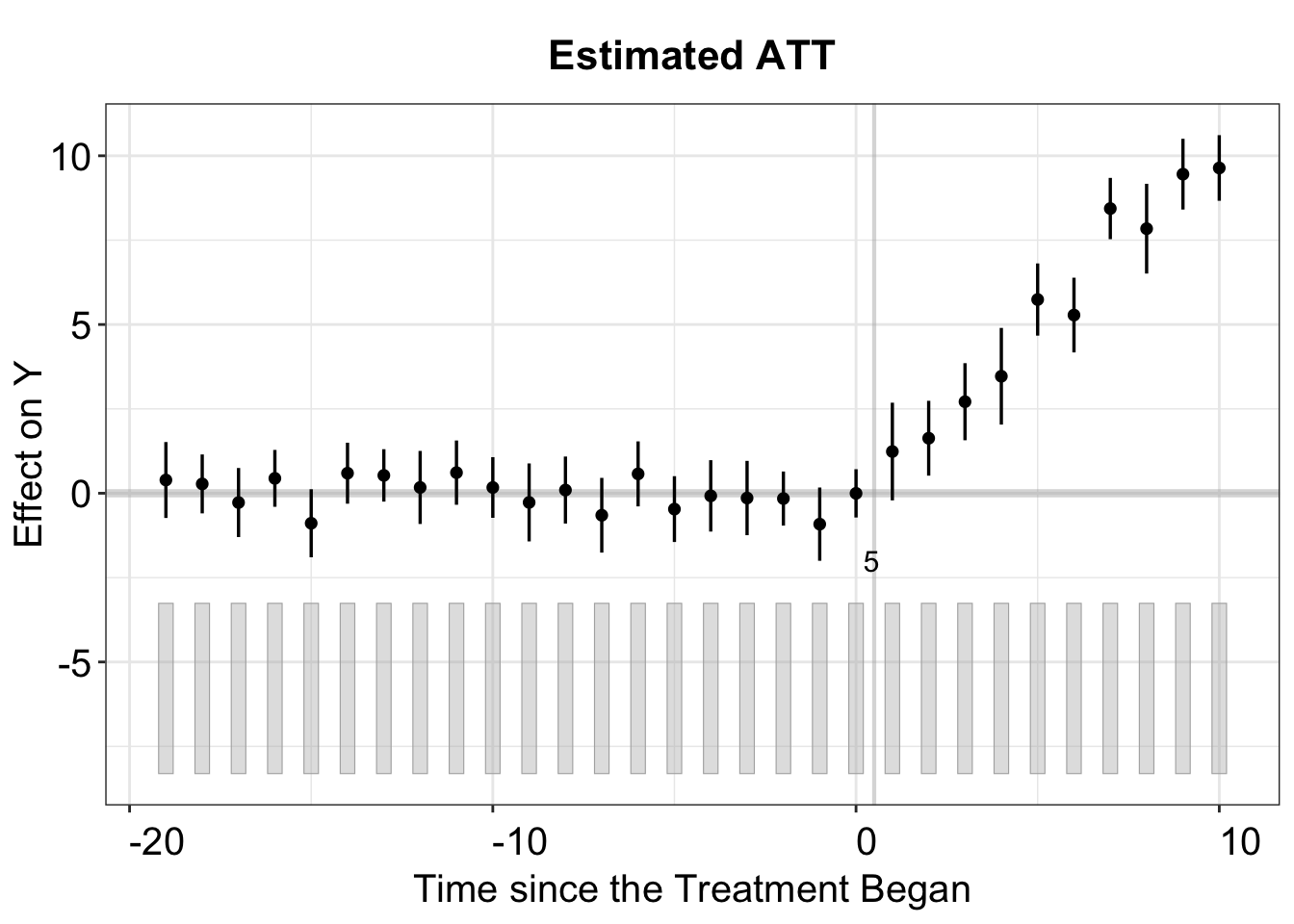
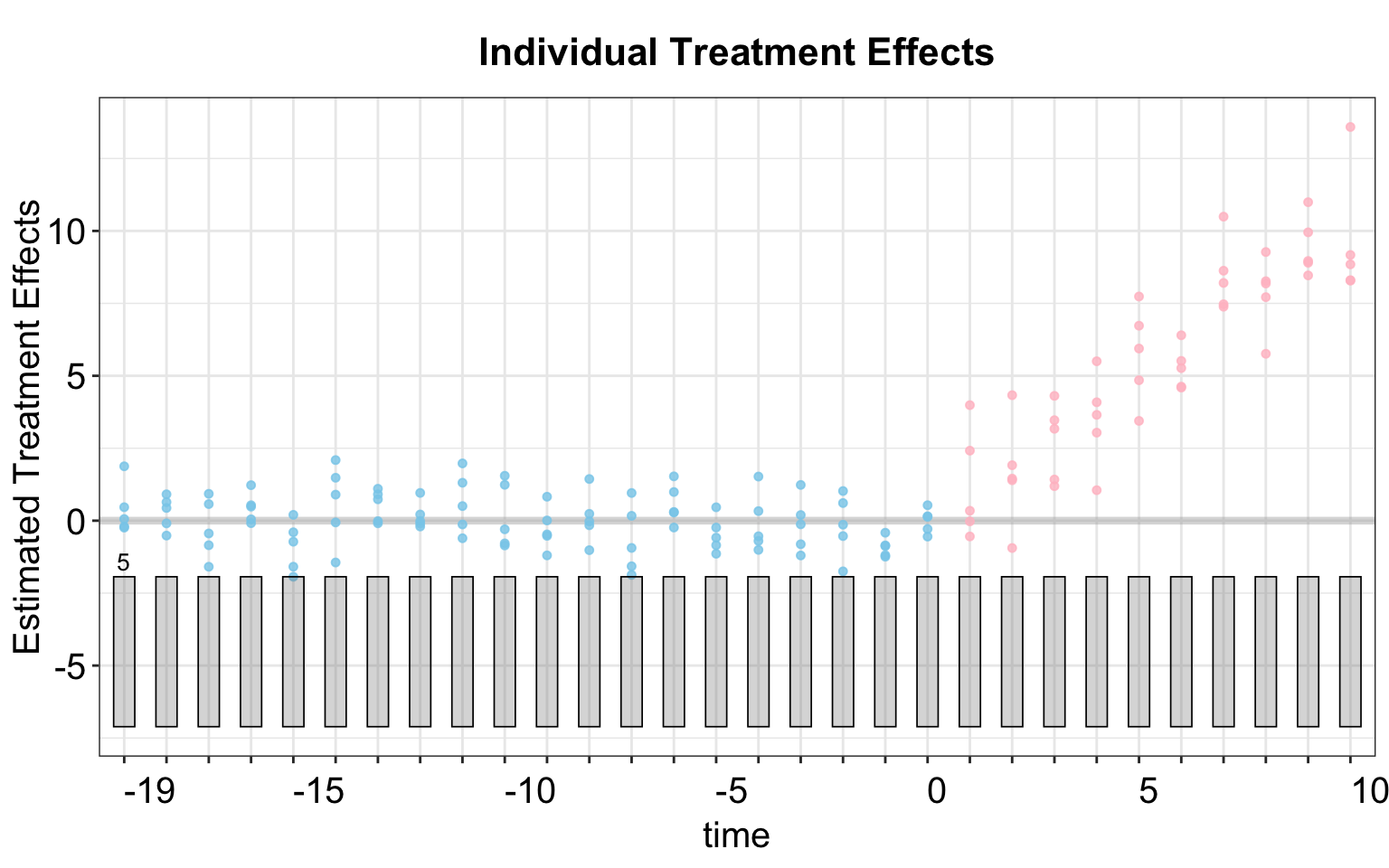
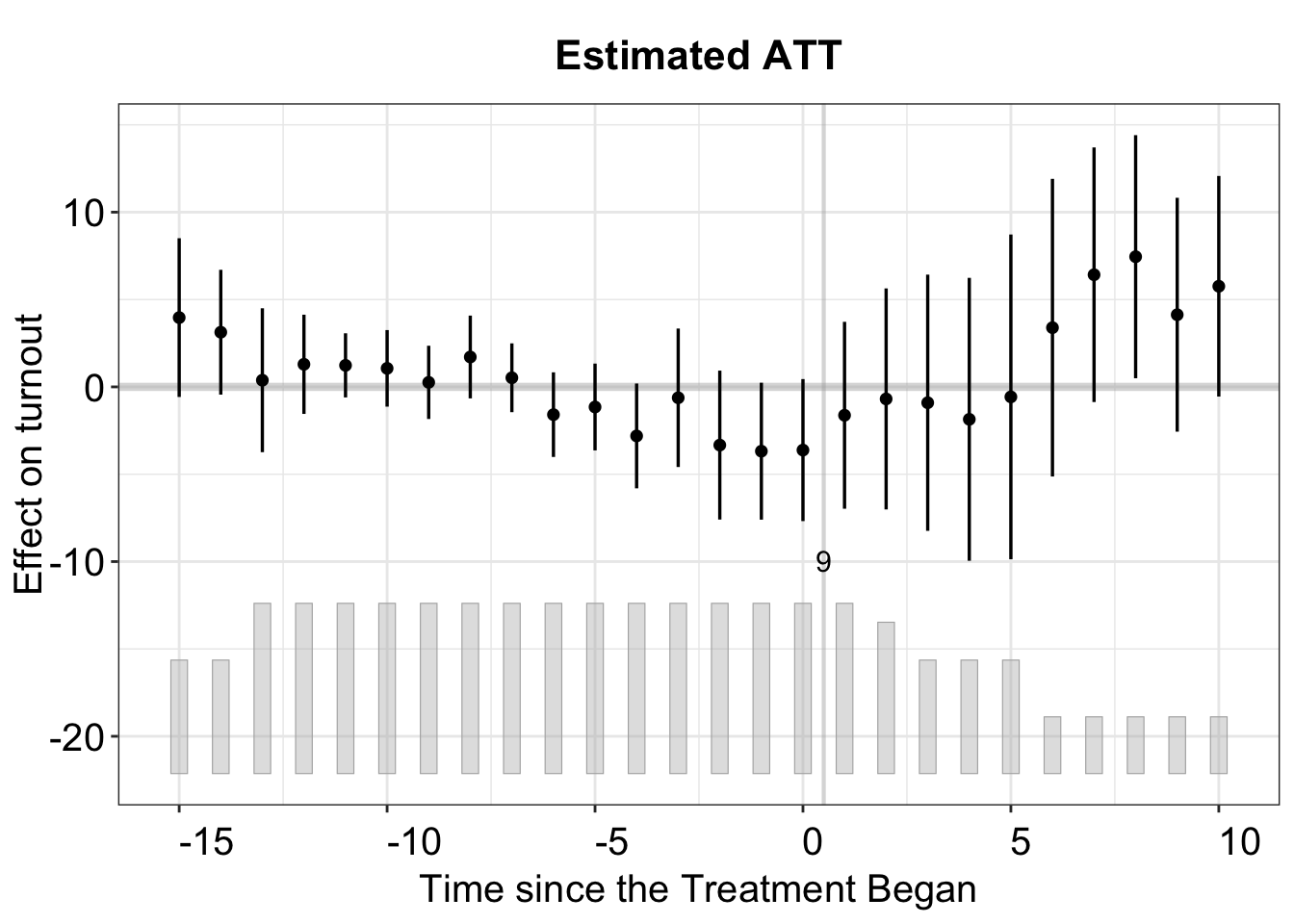
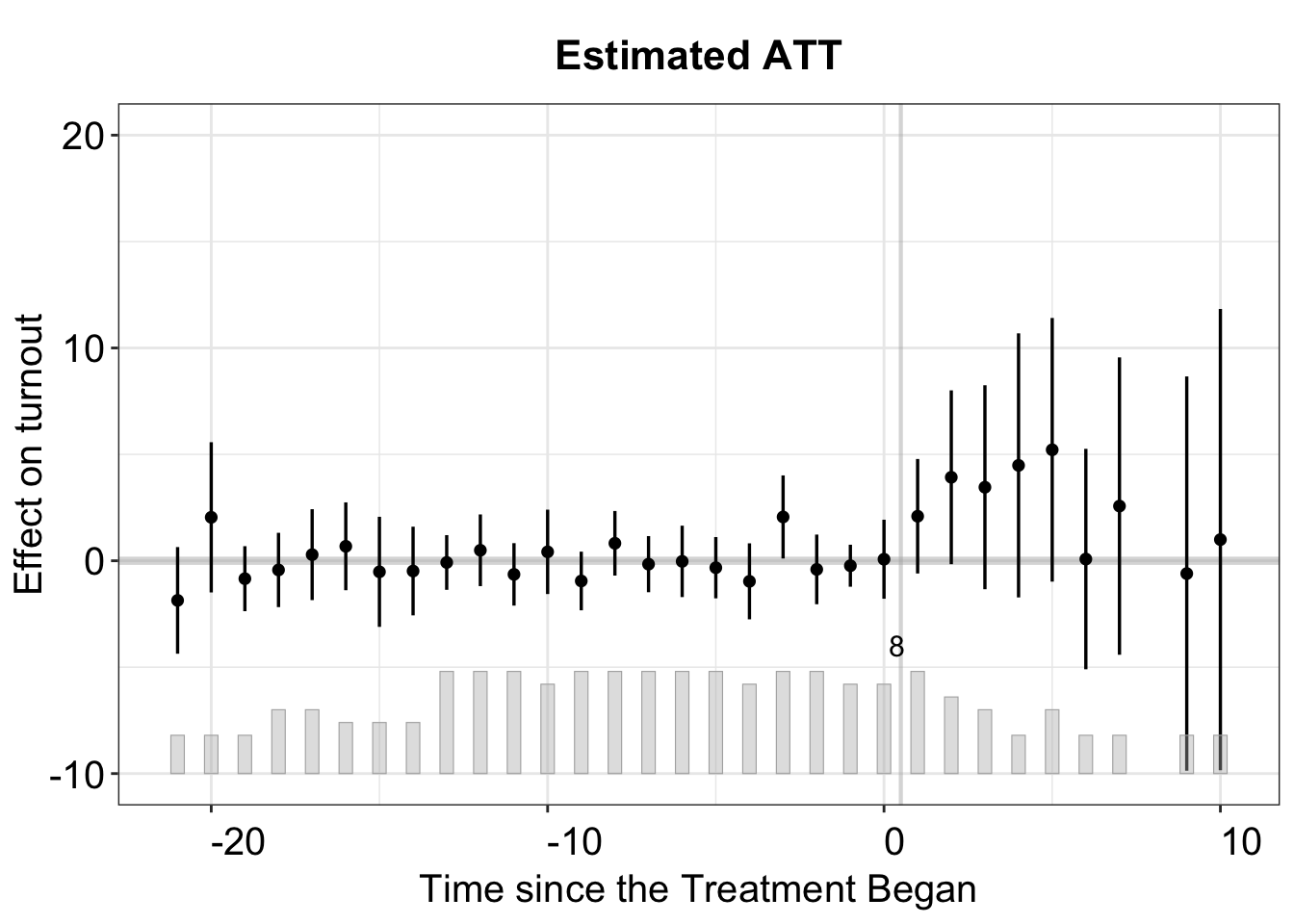
By default, the print function produces a gap plot, equivalent to using plot(out, type = "gap"), and visualizes the estimated Average Treatment Effect on the Treated (ATT) by period. For reference, the true effects in gsynth range from 1 to 10 (with some added white noise) and take effect during periods 21 to 30.

Note that the plot() generates a ggplot2 object, which users can save by simply calling print with the object’s name.

a <- plot(out) # by default, type = "gap"
print(a)

Setting theme.bw = FALSE sets the plotting style to the default ggplot2 theme.

plot(out, theme.bw = FALSE)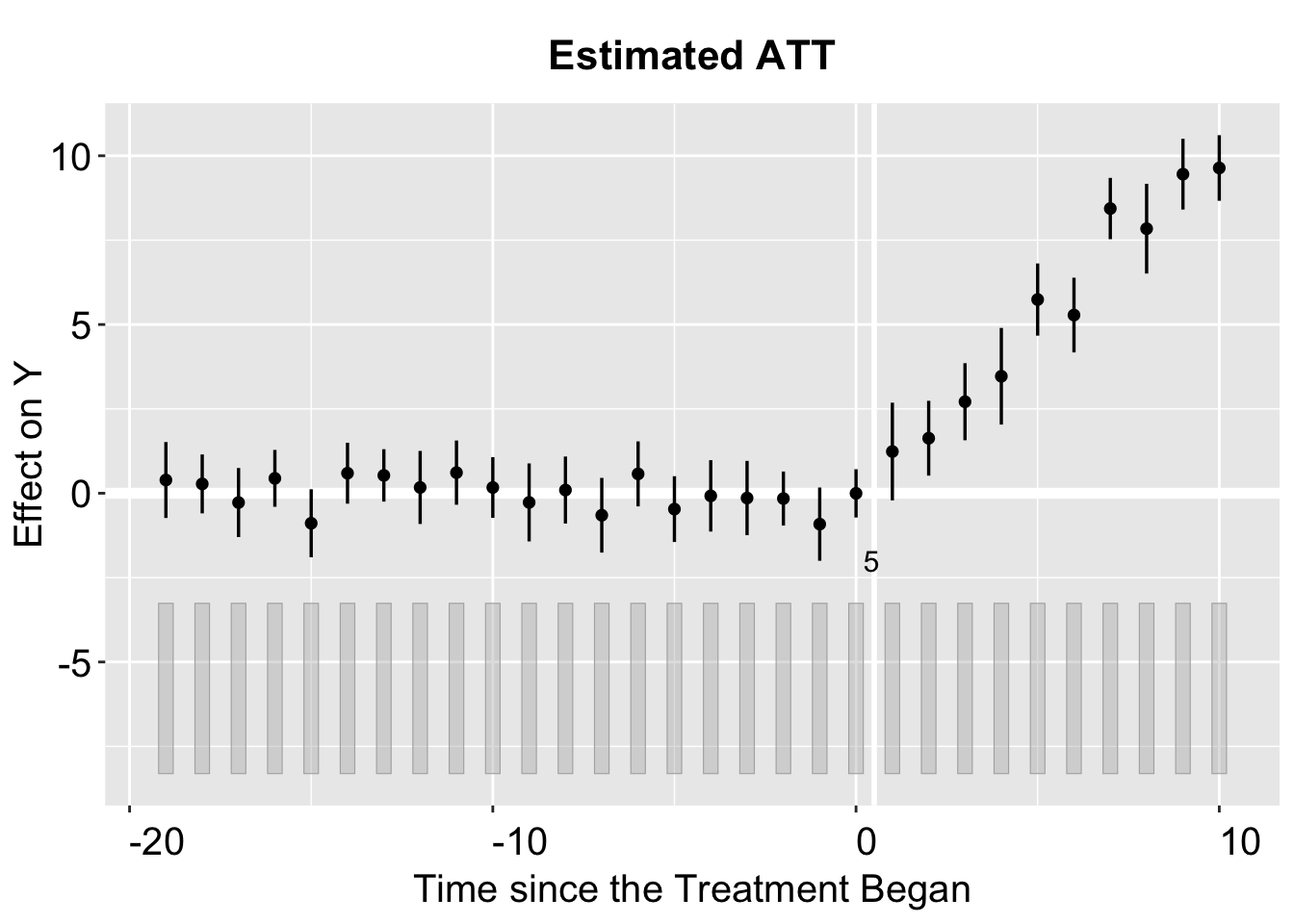 

By switching off show.points, the confidence interval of the ATT estimates will be represented by a shaded area.

plot(out, show.points = FALSE)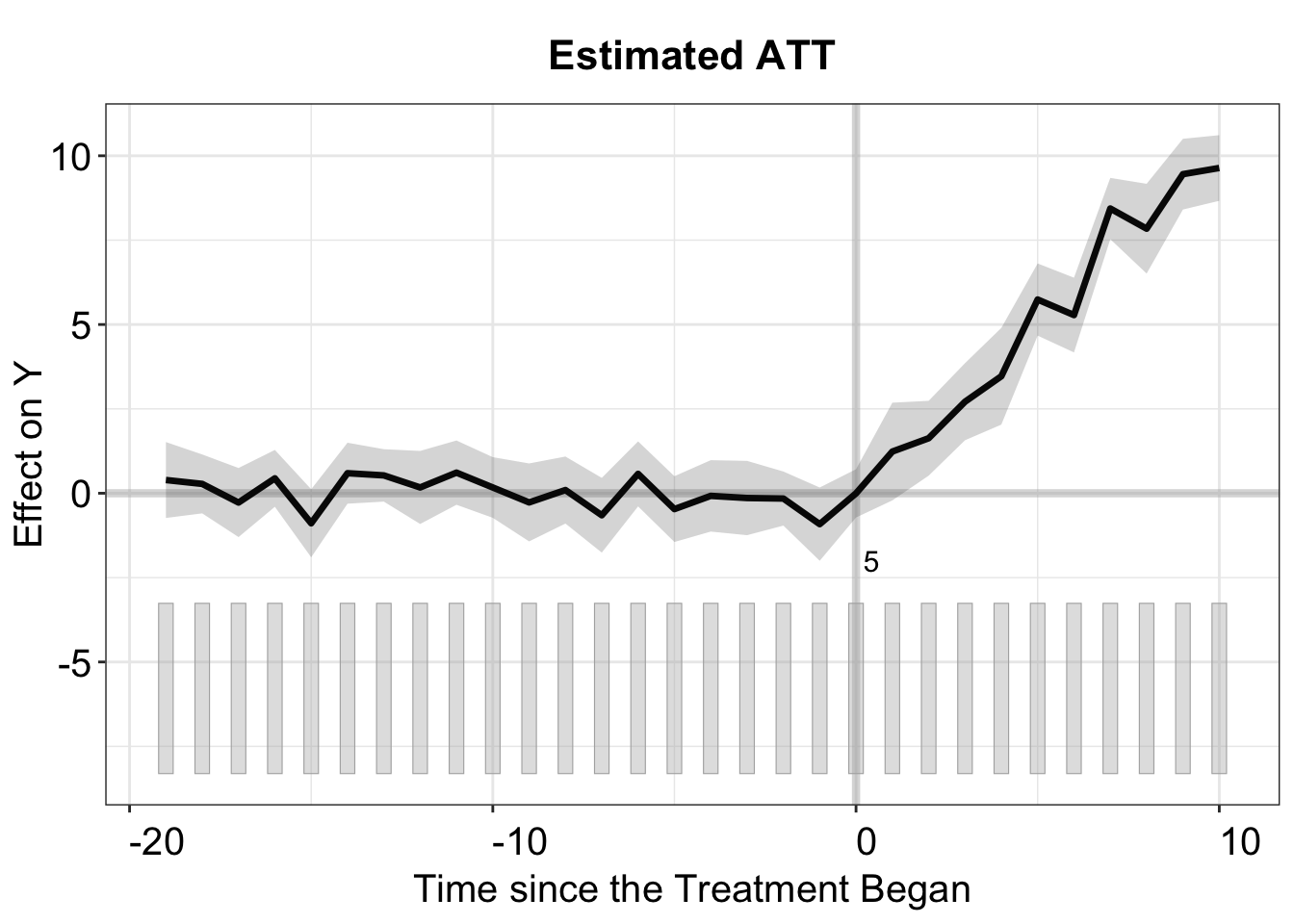 

Aesthetic options for ggplot2 objects are compatible for all fect plots.

For demonstration, we use main, xlim, and ylim to set the plot title and axis labels.

plot(out, type = "gap", ylim = c(-3,12), xlab = "Period", 
     main = "Estimated ATT (FEct)")

fect objects can generate eight types of plots for diverse demonstration purposes. The type option includes the following:

• "gap": Reports ATT by period (default).
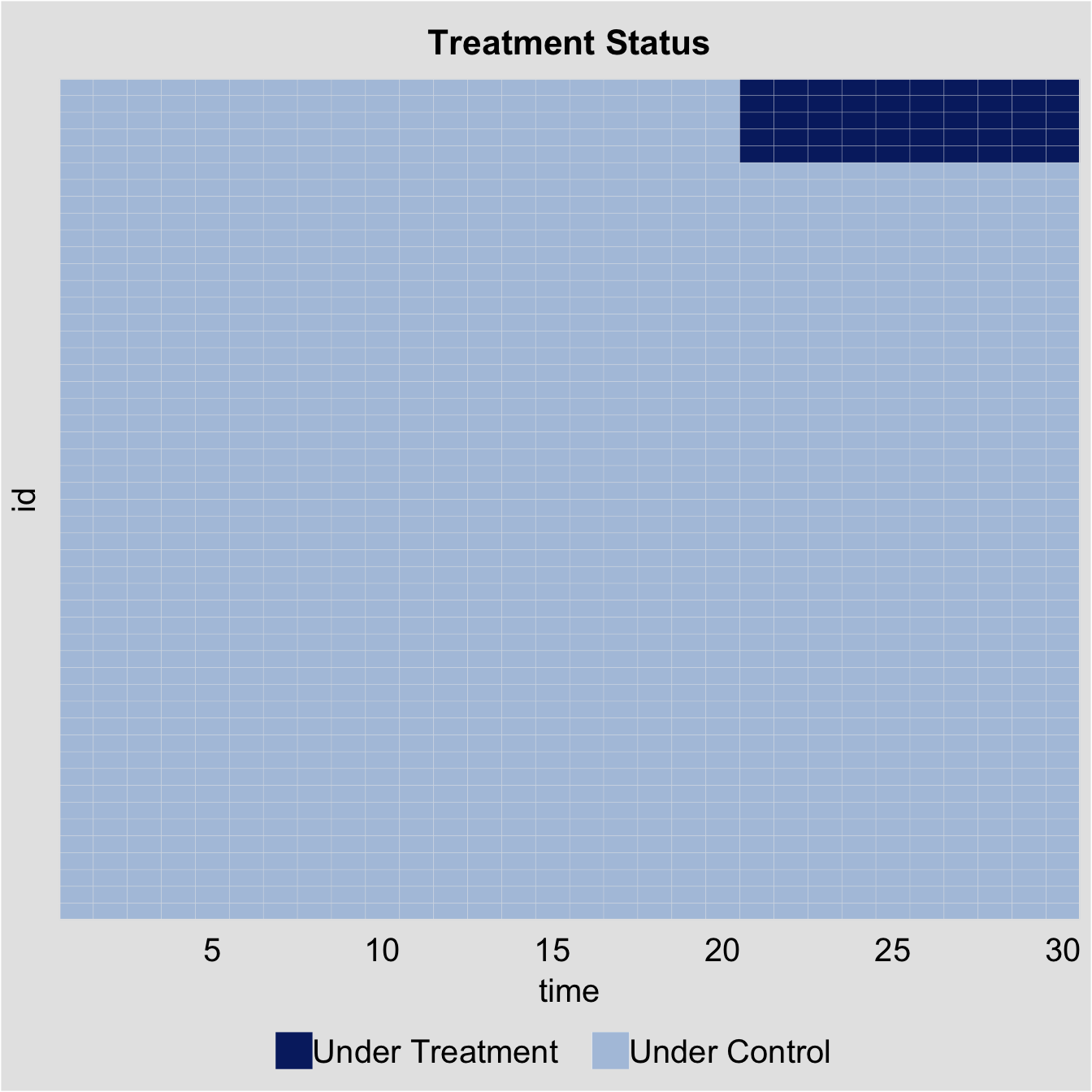
• "status": Plots treatment status of all observations, similar to panelview(). The time labels are displayed only when axis.lab = "time" is set.
• "box": Displays the estimated individual treatment effects with box plot.
• "calendar": Shows how the treatment effect evolves over time.
• "factors" and "loadings": Plot the estimated factors and loadings, respectively.
• "counterfactual": Generates the observed treated outcome alongside the imputed counterfactual averages. The style can be modified with raw = "all" for linear or raw = "band" for graphic representation of all estimated counterfactual results.
• "equiv": Exhibits the average pretreatment residuals with equivalence confidence intervals.

The figure below illustrates the treatment status of all observations. Users can specify the exact values shown on the x- and y-axes using the xticklabels and yticklabels parameters (i.e., xticklabels=c("1","5","10", "15","20", "25", "30")). Setting a nonexistent value to the option removes all numeric labels for that axis (i.e., yticklabels="0"). The status plot has now been incorporated into a standalone package, panelView.

plot(out, type = "status", yticklabels="0", 
     xticklabels=c("5", "10", "15","20", "25", "30") )

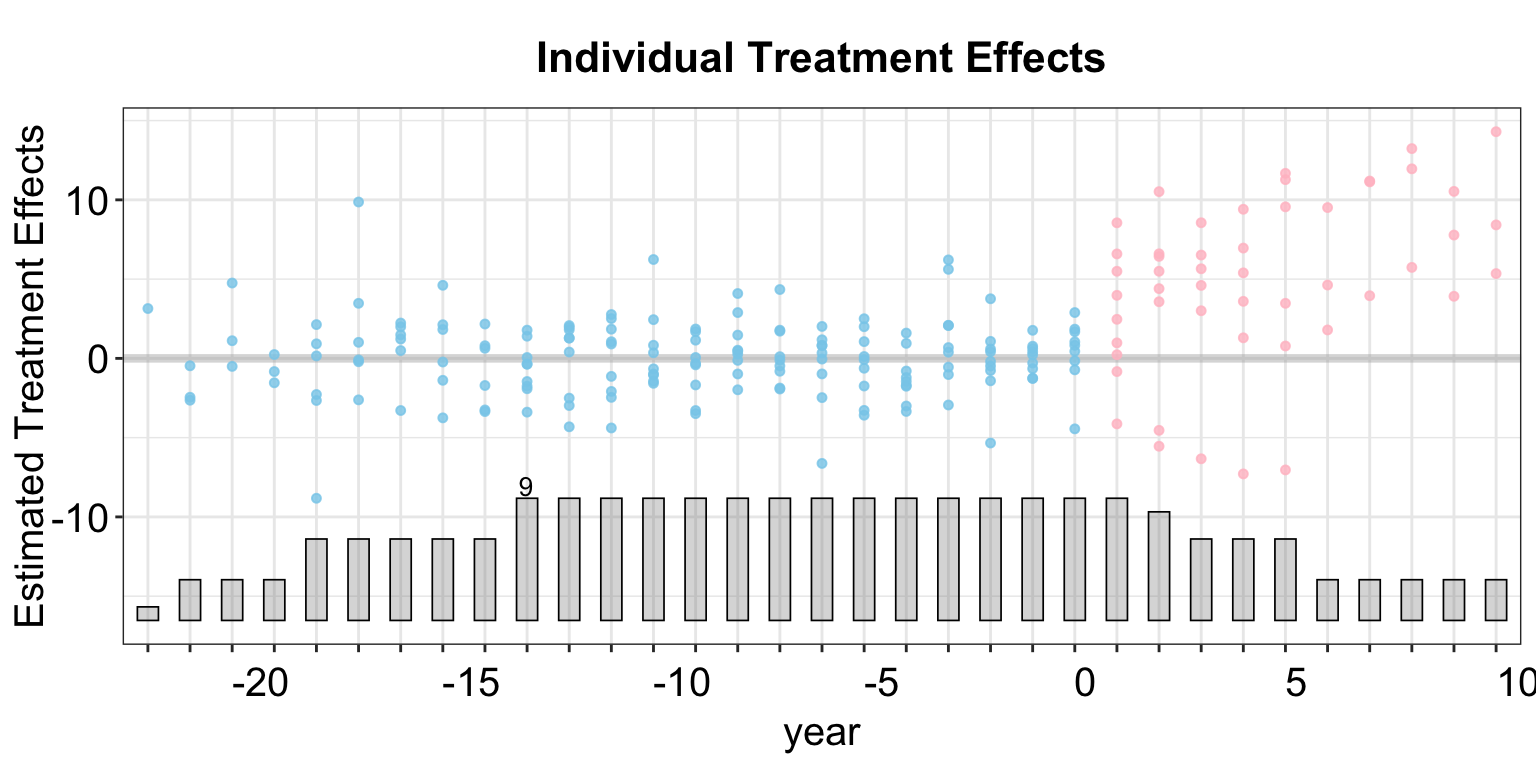
The box plot visualize the estimated individual treatment effects for the treated units. While these effects are not identified at the individual level, their dispersion provides insight into heterogeneous treatment effect across different time periods and informs model performance. By default, the number of total treated units is labeled on the graph. Note, if the number of treated units is small, the box plot will reduce to a scatter plot, as shown below.

We also provide the xangle and yangle options to allow users to tilt the labels for better display. We will demonstrate the functionality in later examples.

plot(out, type = "box", xlab = "time",
     xticklabels=c("-19", "-15", "-10", "-5","0","5","10") )

If we want to focus on specific periods within the full panel, the xlim option is useful. Here, we narrow the time frame to fifteen periods before and ten periods after the treatment.

plot(out, type = "box", xlim = c(-15, 10), 
     xticklabels=c( "-15", "-10", "-5","0","5","10"))

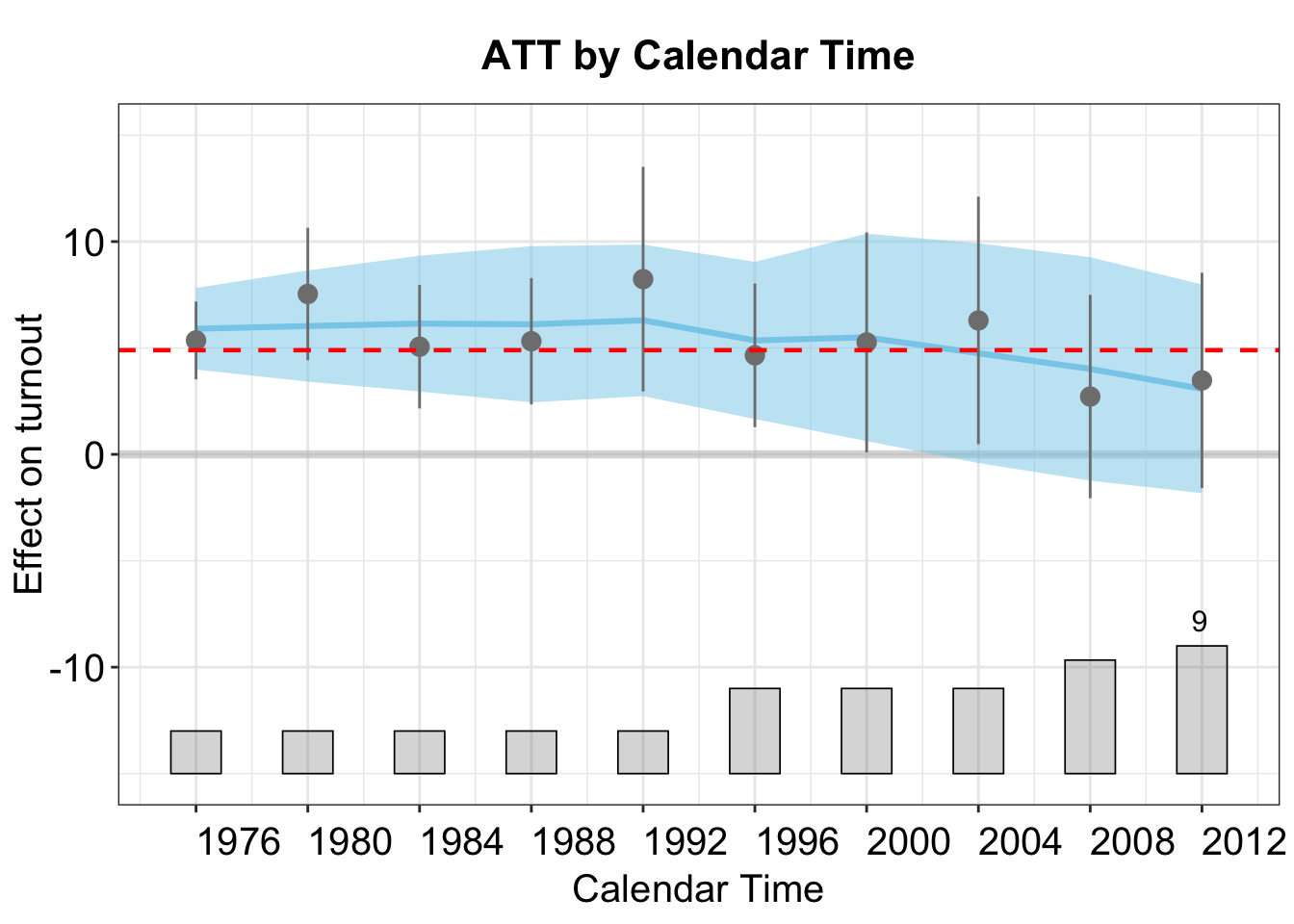
To explore how the treatment effect evolves over time, we can set type = "calendar".

In the plot below, the points represent the ATTs by calendar time. The blue curve shows a lowess fit of these estimates, with the shaded band indicating the 95% confidence interval. The red horizontal dashed line marks the overall average ATT across all time periods.

plot(out,type = "calendar")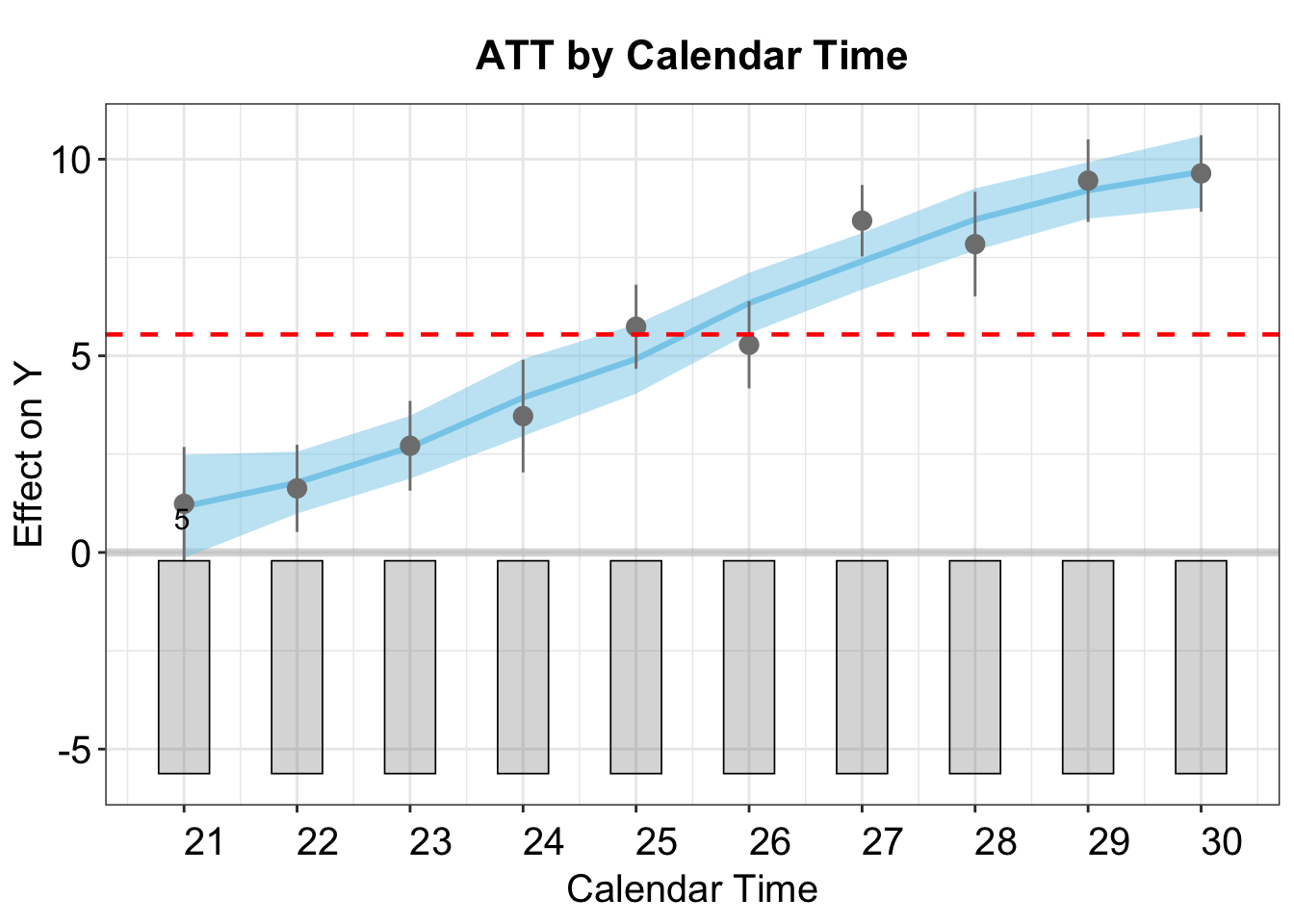

The next two figures plot the estimated factors and factor loadings, respectively.

plot(out, type = "loadings")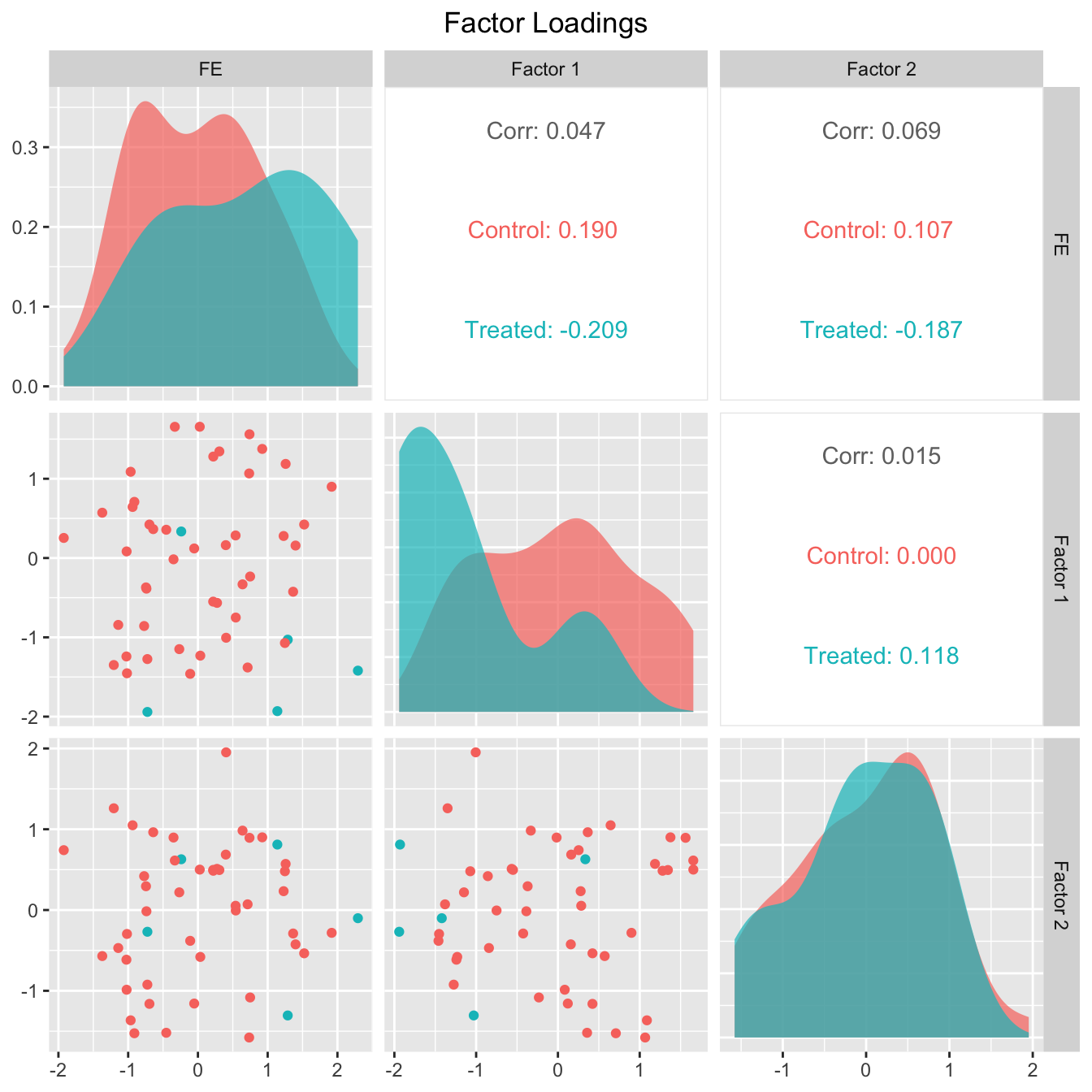

plot(out, type = "factors", xlab = "Time")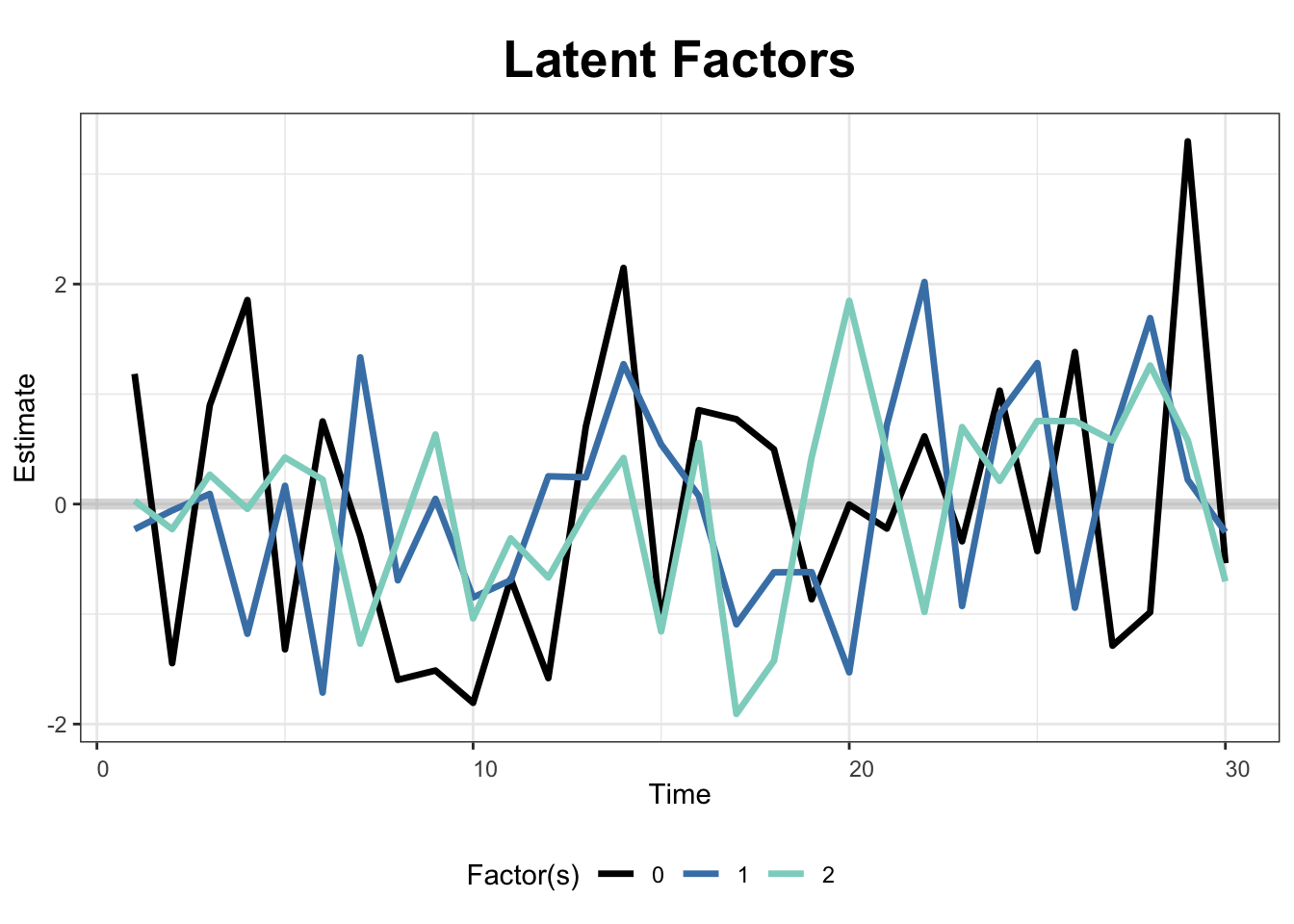

To visualize the estimated counterfactual outcomes, we use type = "counterfactual". If no argument is assigned to raw, the plot will display the average of the treated and of the estimated counterfactual outcomes.

plot(out, type = "counterfactual")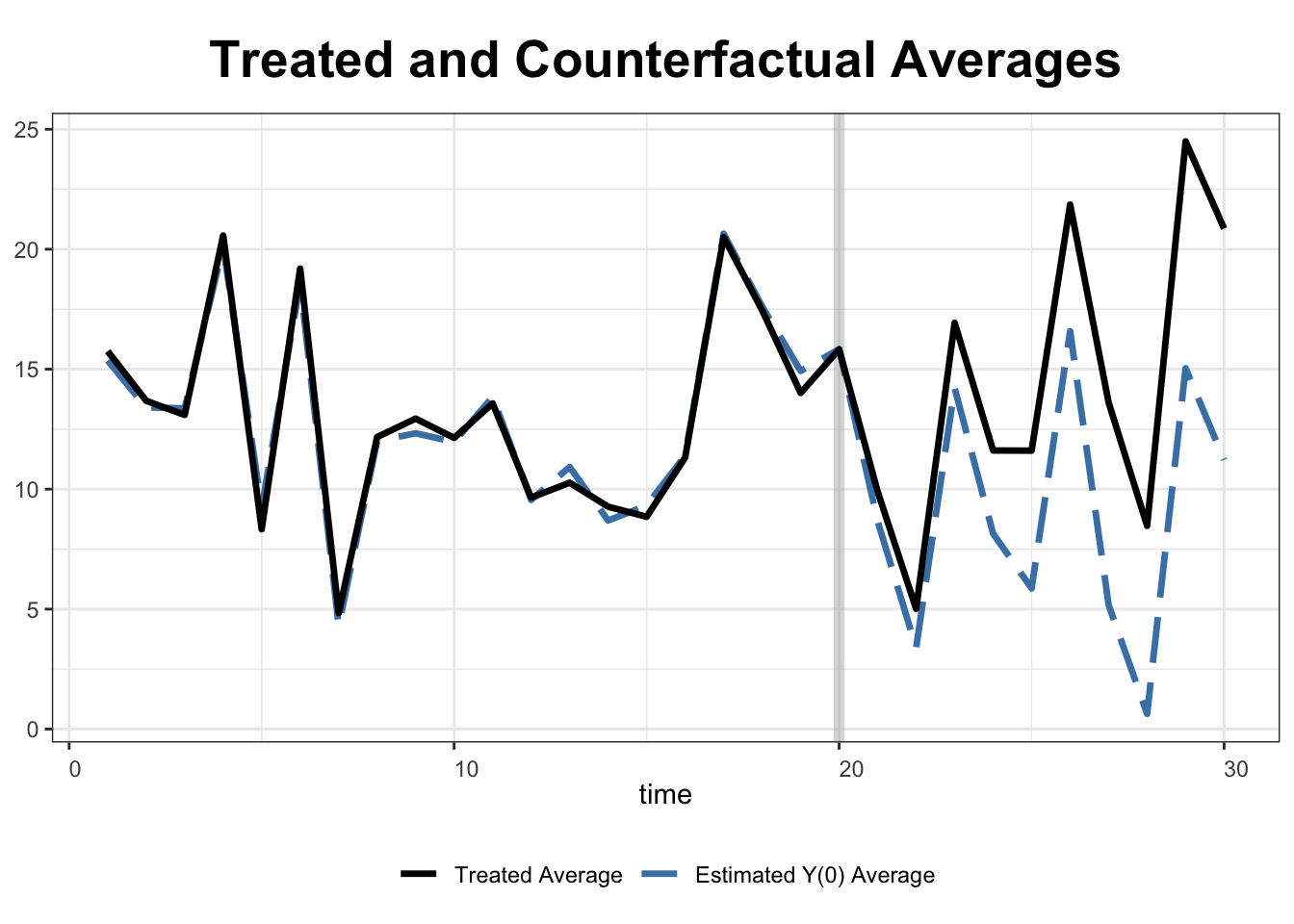

fect offers two options for displaying all estimated counterfactual estimates: raw="all" for linear and raw="band" for a graphical (shaded band) representation.

plot(out, type = "counterfactual", raw = "all")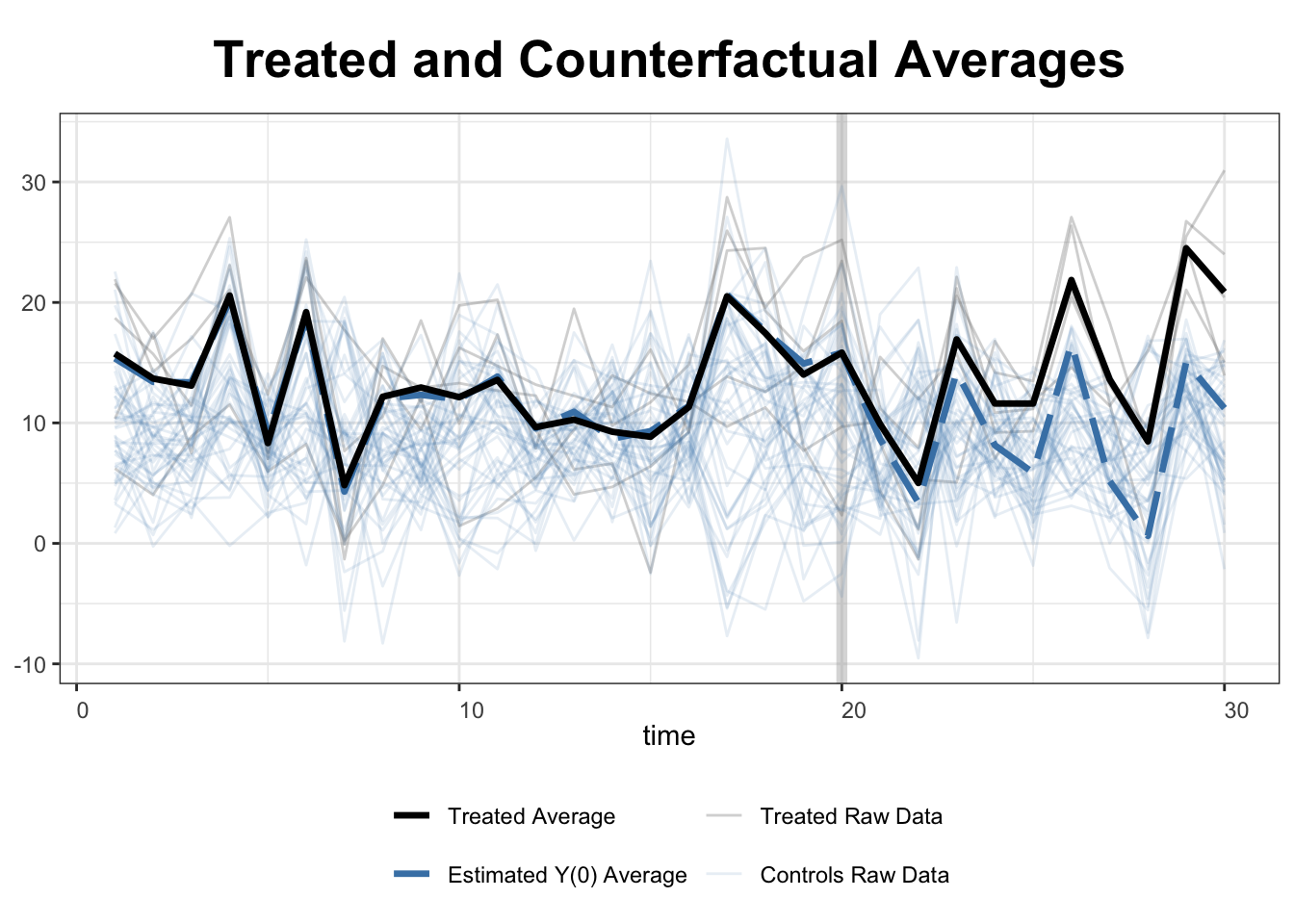

plot(out, type = "counterfactual", raw = "band")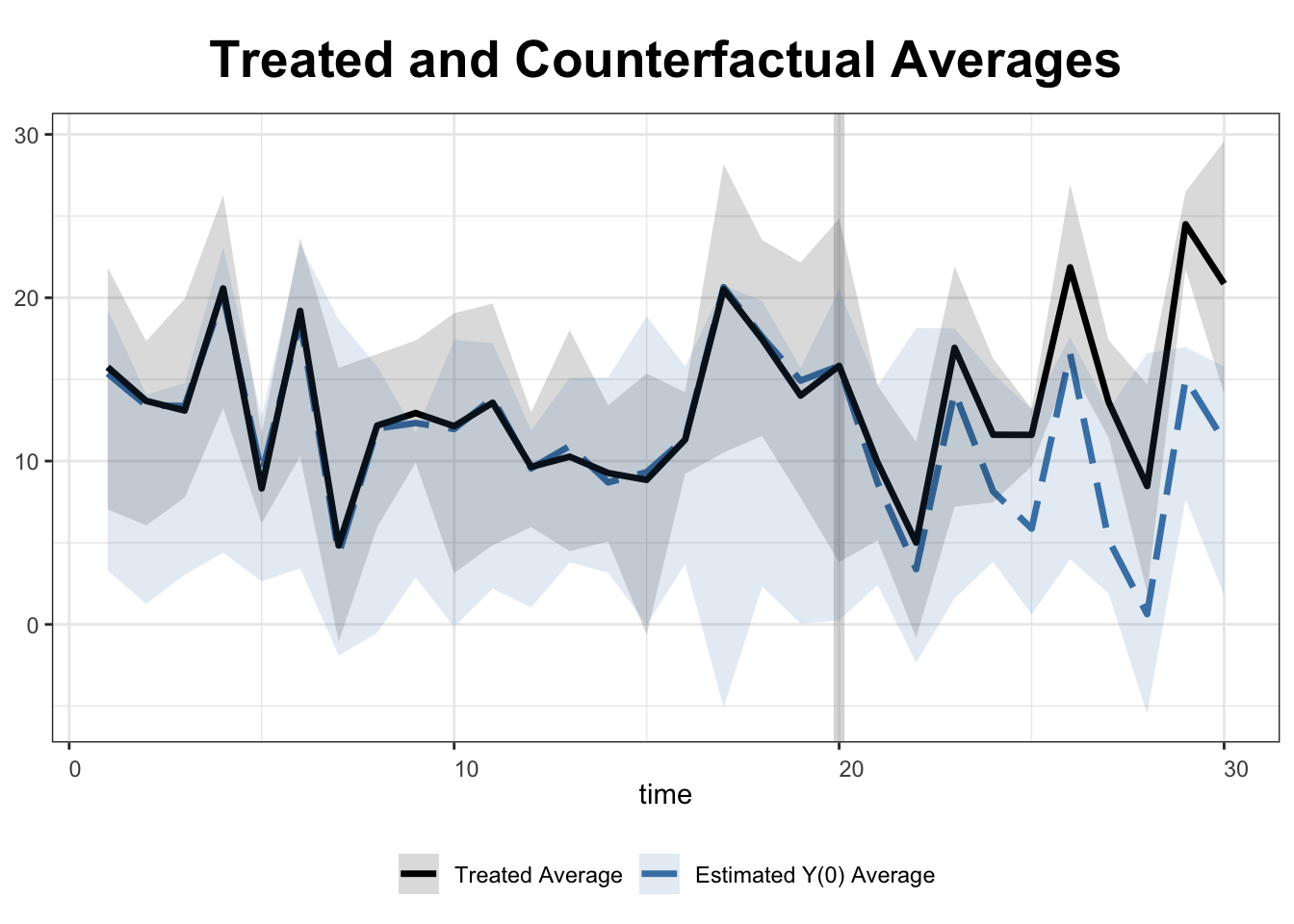

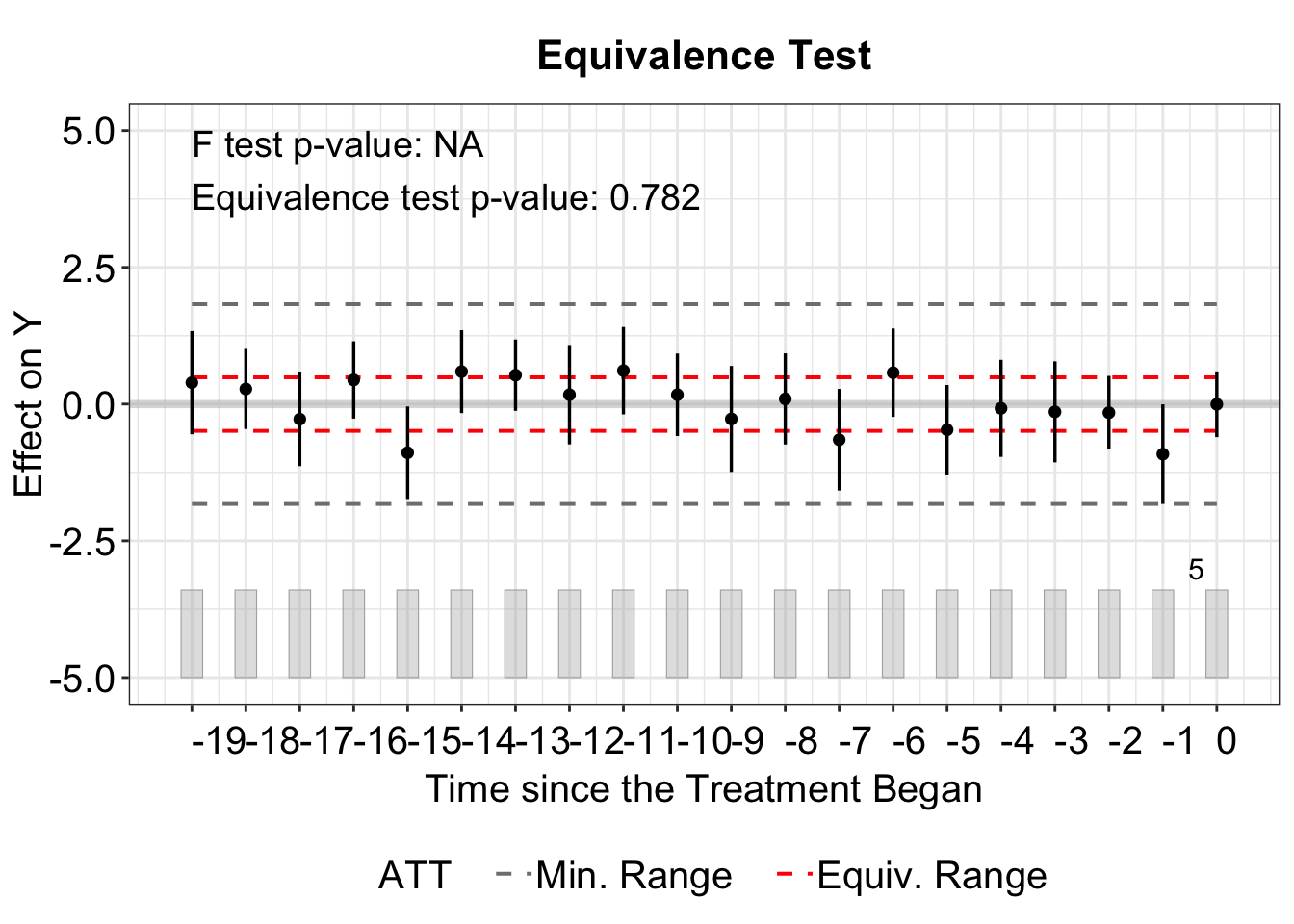
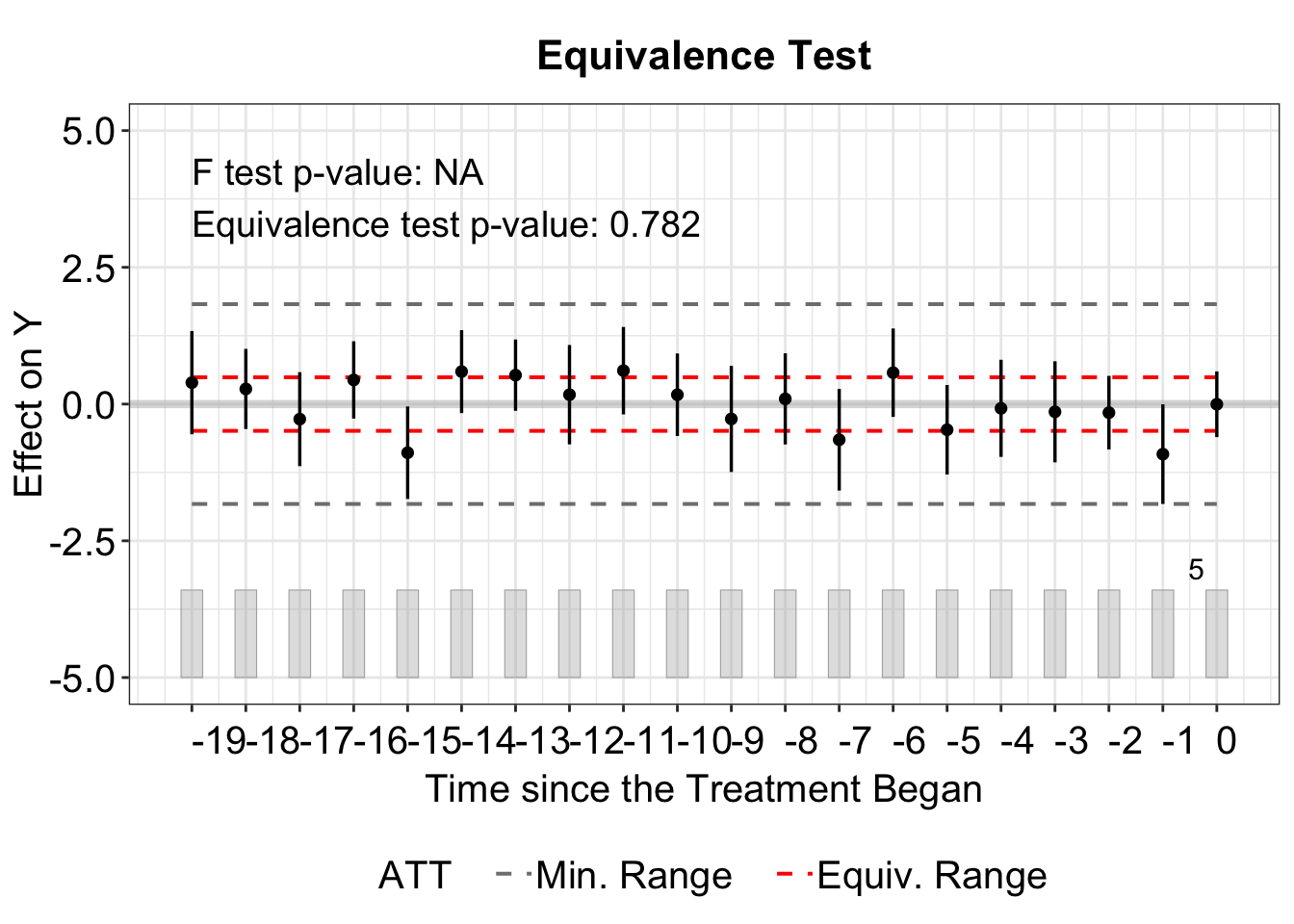
Lastly, type = "equiv" helps visualize the average pretreatment residuals with equivalence confidence intervals.

plot(out, type = "equiv", ylim = c(-5, 5))

The floating legend displaying the F-test p-value and Equivalence test p-value can be removed by setting show.stats = FALSE.

plot(out, type = "equiv", show.stats =  FALSE)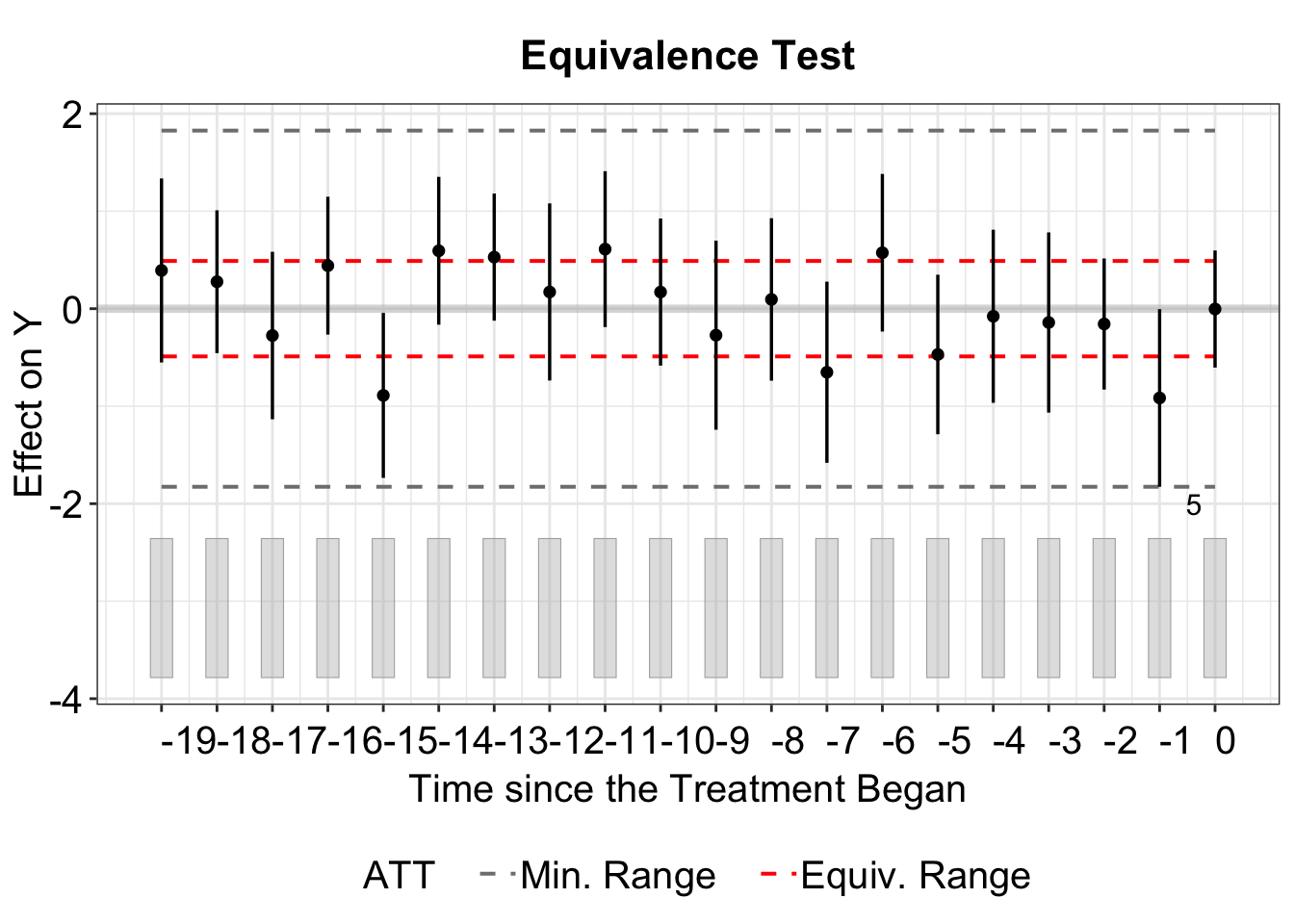

Alternatively, it can be repositioned by providing coordinates to stats.pos.

plot(out, type = "equiv", stats.pos = c(-19, 4.5), ylim = c(-5, 5))

3.4 Comparing w/ IFEct & MC

Since we have now merged gysnth into fect, the original ife and mc methods in gysnth now can be directly implemented in fect. Please refer to the previous chapter for implementation details.

Here, we apply these two methods to the simulated dataset simgsynth and compare the results from those from setting method = "gysnth". Note that not only the algorithms are (slightly) different, the inferential methods are different, too. Both ife and mc use large-sample inferential method such as nonparametric bootstrap or jackknife while gsynth employs a two-step parametric bootstrap procedure, analogous to conformal inference, which accommodates a small number of treated units.

3.4.1 IFEct

For the ife method, we need to specify an interval of candidate number of unobserved factors in option r like r=c(0,5). When cross-validation is switched off, the first element in r will be set as the number of factors. Below we use the MSPE criterion and search the number of factors from 0 to 5.

out.ife <- fect(Y ~ D + X1 + X2, data = simgsynth, index = c("id","time"), 
          force = "two-way", method = "ife", CV = TRUE, r = c(0, 5), 
          se = TRUE, nboots = 200, parallel = TRUE)

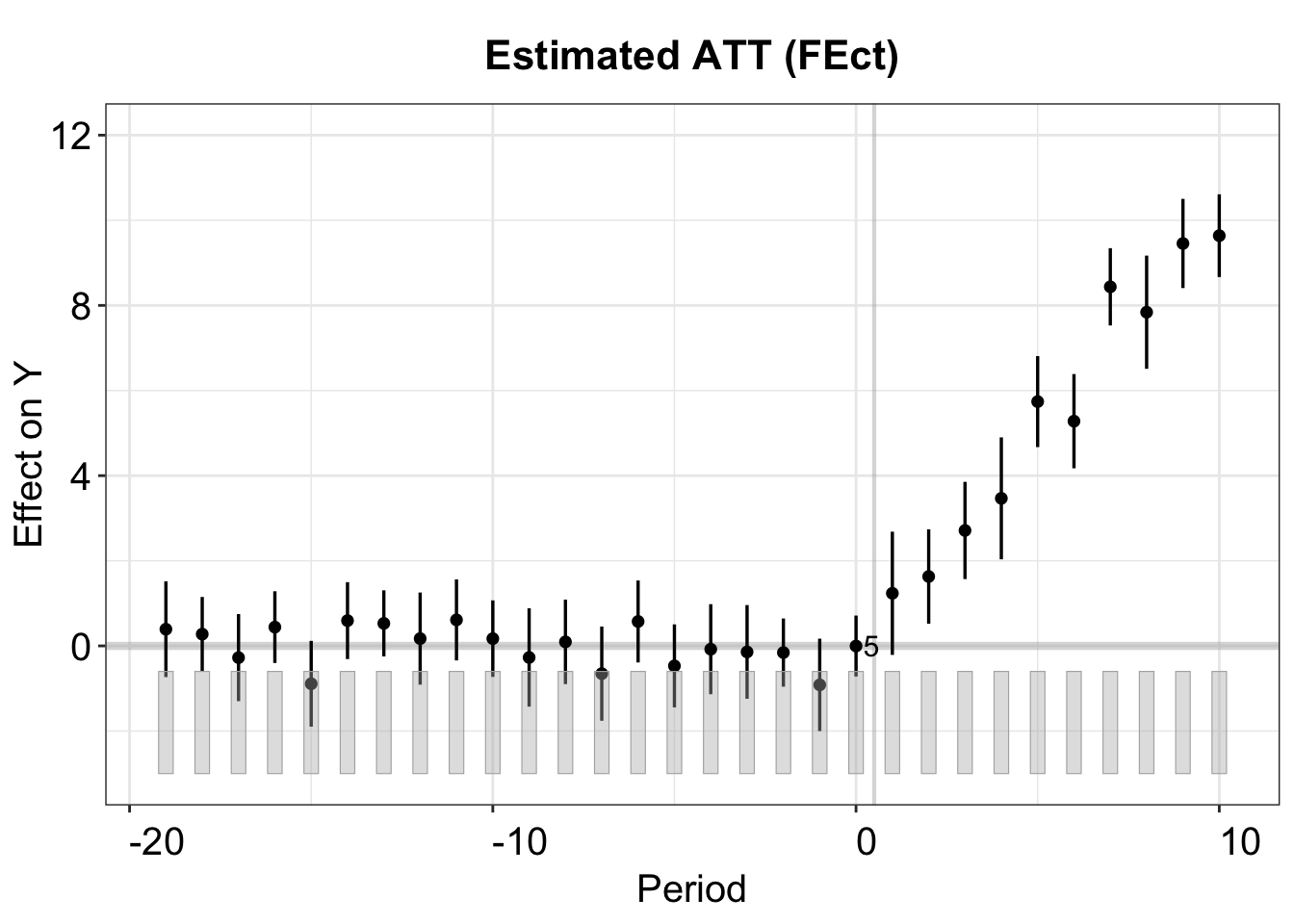
The figure below shows the estimated ATT using the IFE method. The cross-validation procedure selects the correct number of factors \((r=2)\).

plot(out.ife, main = "Estimated ATT (EM)")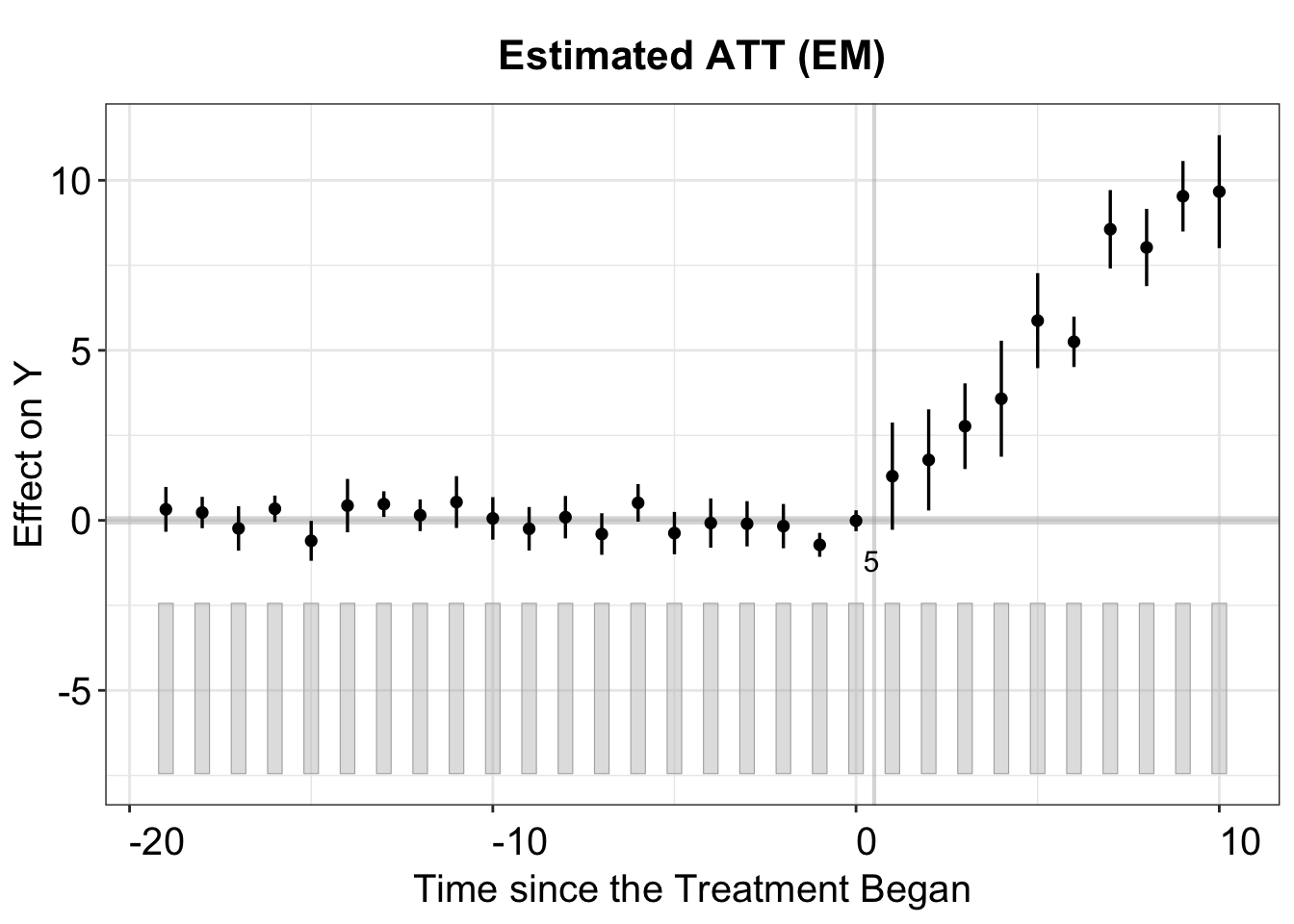

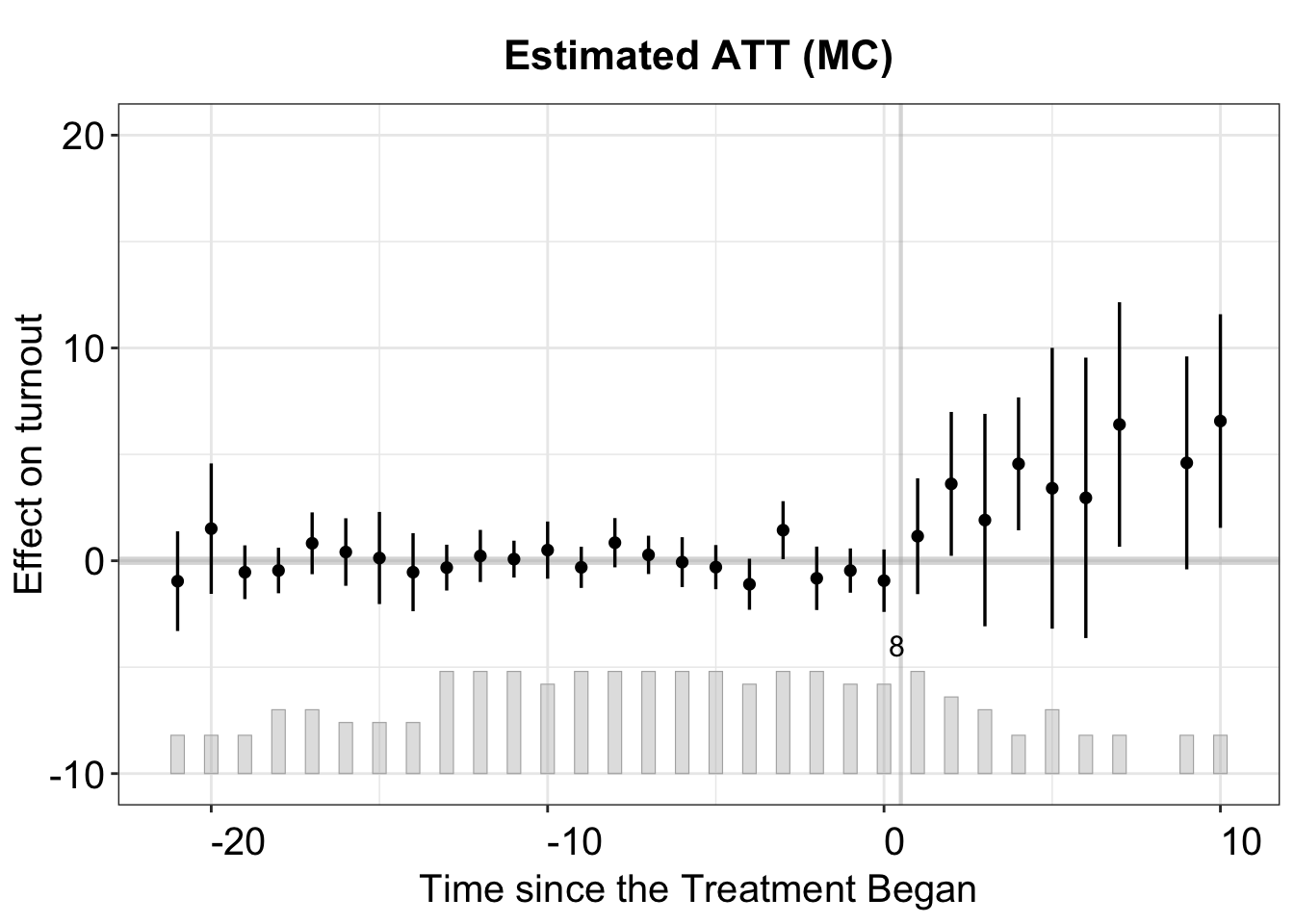
3.4.2 Matrix completion

To implement the MC method, a sequence of candidate tuning parameters must be specified. For example, users can set lambda = c(1, 0.8, 0.6, 0.4, 0.2, 0.05). If lambda is not specified, fect uses an algorithm to automatically generate a set of candidate tuning parameters based on the outcome variable. Users can adjust the number of tuning parameters with nlambda, which defaults to nlambda = 10.

out.mc <- fect(Y ~ D + X1 + X2, data = simgsynth, 
               index = c("id","time"), 
                force = "two-way", method = "mc", CV = TRUE, 
                se = TRUE, nboots = 200, parallel = TRUE)
#> Parallel computing ...
#> Cross-validating ...
#> Criterion: Mean Squared Prediction Error
#> Matrix completion method...
#> lambda.norm = 1.00000; MSPE = 2.48330; MSPTATT = 0.69437; MSE = 1.97846
#> lambda.norm = 0.42170; MSPE = 1.86775; MSPTATT = 0.31226; MSE = 1.02780
#> *
#> lambda.norm = 0.17783; MSPE = 1.97214; MSPTATT = 0.09063; MSE = 0.31477
#> lambda.norm = 0.07499; MSPE = 2.14644; MSPTATT = 0.01738; MSE = 0.06379
#> lambda.norm = 0.03162; MSPE = 2.28420; MSPTATT = 0.00308; MSE = 0.01170
#> 
#>  lambda.norm* = 0.421696503428582
#> 
#> Bootstrapping for uncertainties ...
#> 200 runs
#> Cannot use full pre-treatment periods in the F test. The first period is removed.

plot(out.mc, main = "Estimated ATT (MC)")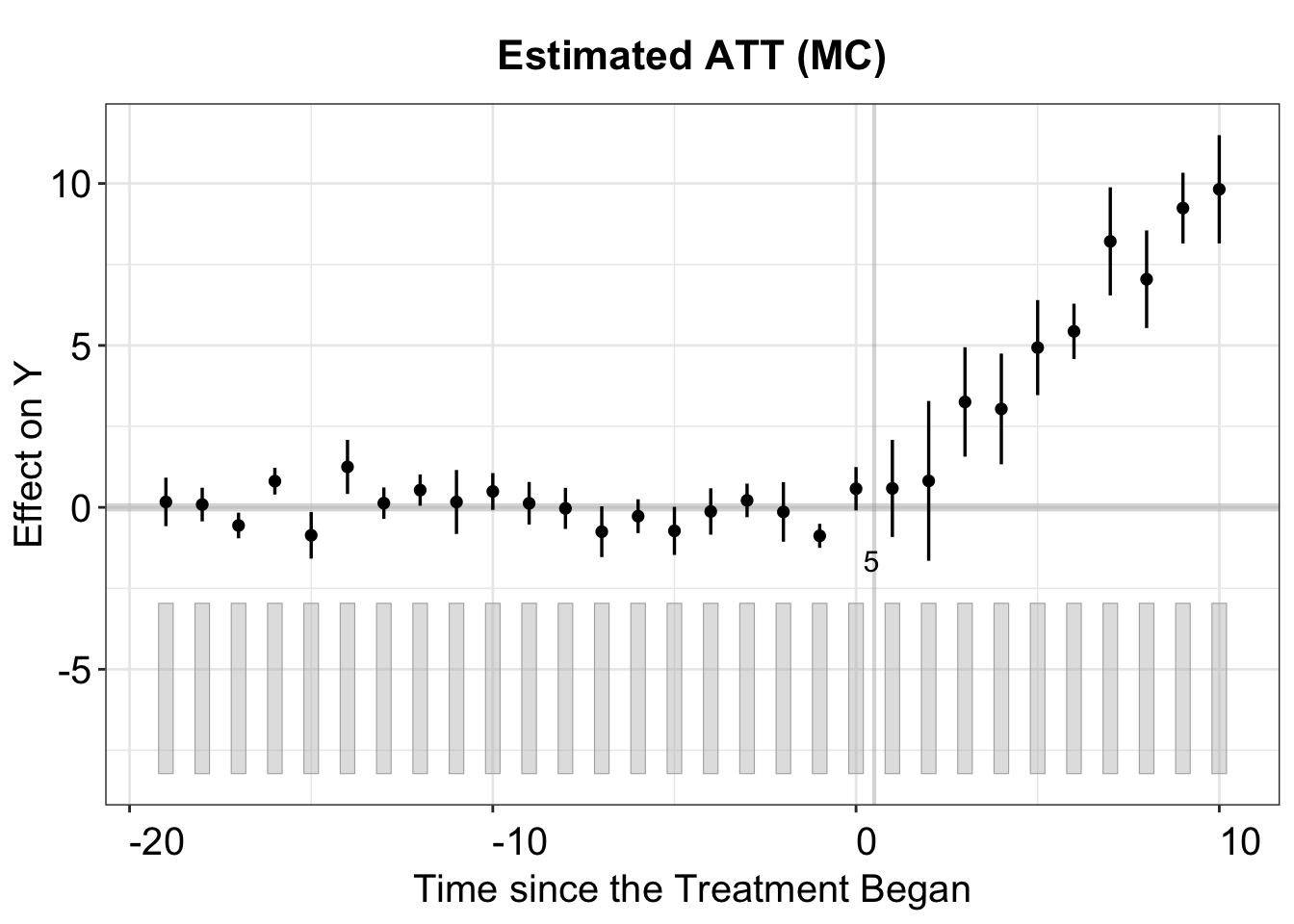

---

3.5 Staggered DID

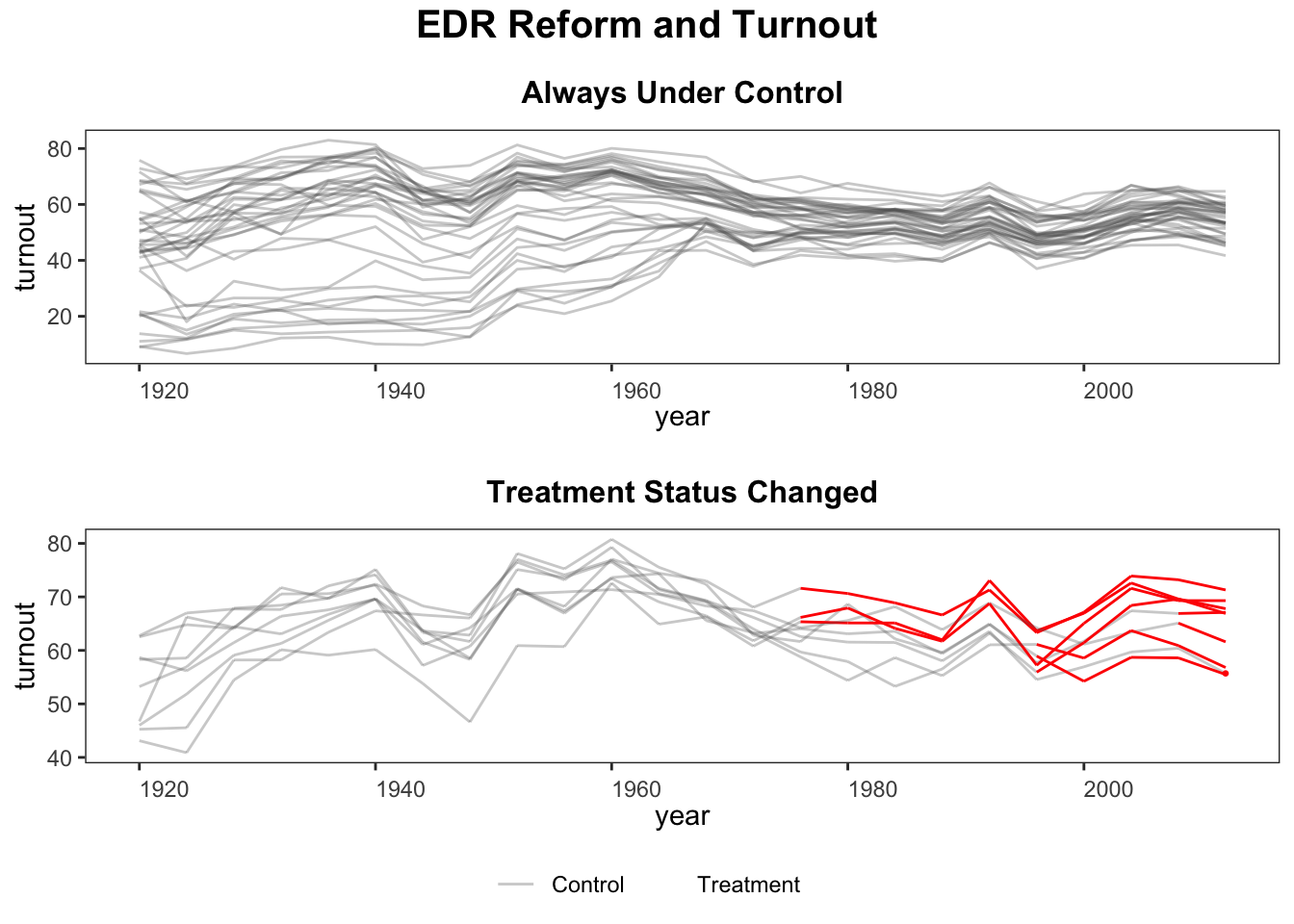
The second example examines the impact of Election-Day Registration (EDR) reforms on voter turnout in the United States, with the treatment taking effect at varying times across states. Further details about the dataset can be found in the Xu(2017) Section 5.

3.5.1 Data structure

First, we use panelView to visualize the data structure. The following figure shows that (1) we have a balanced panel with 9 treated units and (2) the treatment starts at different time periods.

panelview(turnout ~ policy_edr, data = turnout, 
          index = c("abb","year"), pre.post = TRUE, 
          by.timing = TRUE)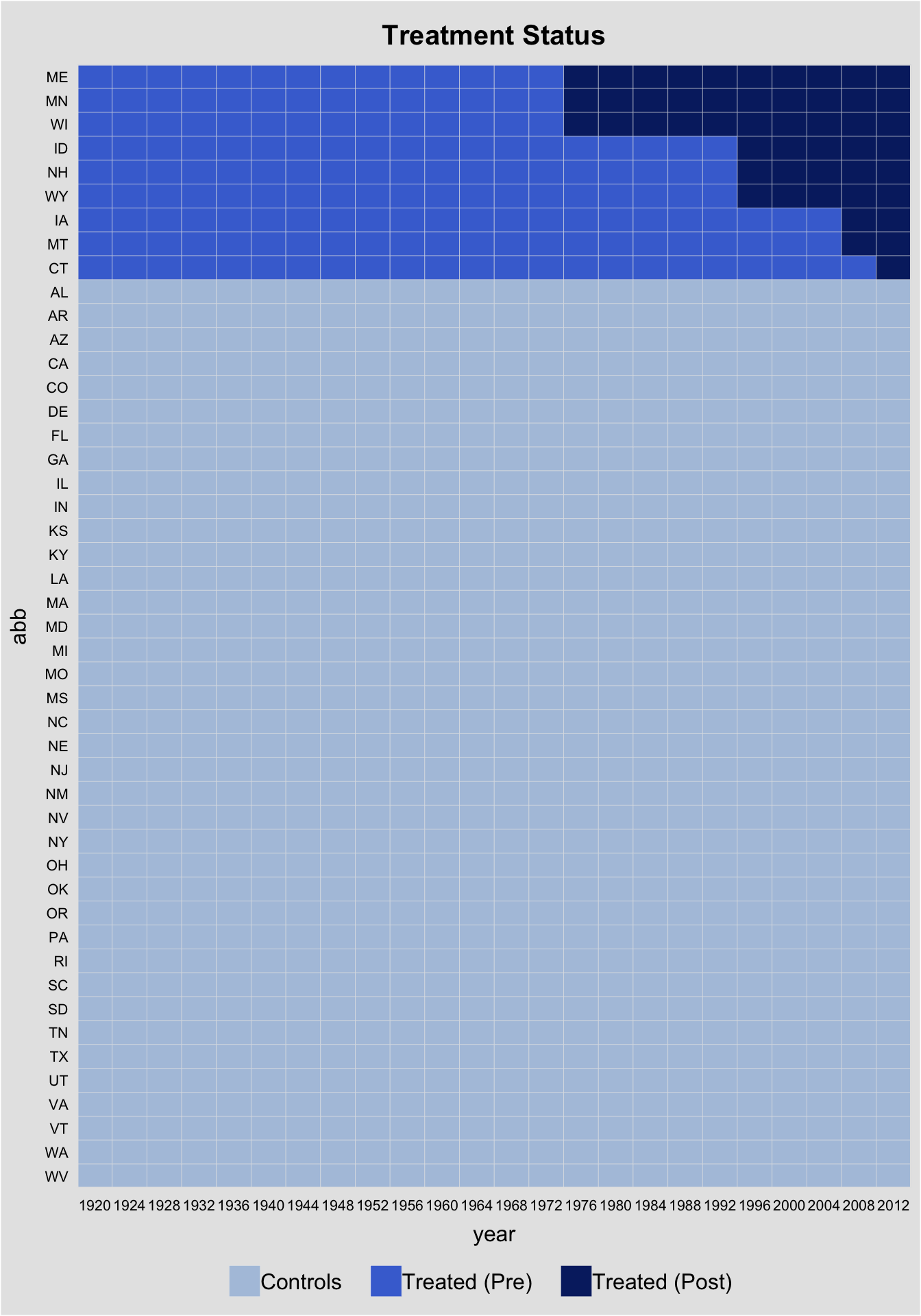 

panelView can visualize the outcome variable by group, using colored lines to represent changes in treatment status.

panelview(turnout ~ policy_edr, data = turnout, 
          index = c("abb","year"), type = "outcome", 
          main = "EDR Reform and Turnout", 
          by.group = TRUE)

3.5.2 Estimation w/o factors

When no factor is assumed, the ATT estimates are close to what we obtain from difference-in-differences.

out0 <- fect(turnout ~ policy_edr + policy_mail_in + policy_motor, 
               data = turnout, index = c("abb","year"), 
               se = TRUE, method = "gsynth",
               r = 0, CV = FALSE, force = "two-way", 
               nboots = 1000, seed = 02139)
#> Parallel computing ...
#> Bootstrapping for uncertainties ...
#> 1000 runs

plot(out0, type = "gap", xlim = c(-15, 15))

3.5.3 Estimation w/ factors

We now allow the algorithm to determine the optimal number of factors that best predict the pre-treatment data with cross-validation.

out_turnout <- fect(turnout ~ policy_edr + policy_mail_in + policy_motor, 
              data = turnout,  index = c("abb","year"), 
              se = TRUE, method = "gsynth", 
              r = c(0, 5), CV = TRUE, force = "two-way", 
              nboots = 1000, seed = 02139)
#> Parallel computing ...
#> Cross-validating ...
#> Criterion: Mean Squared Prediction Error
#> Interactive fixed effects model...
#> Cross-validating ...
#> r = 0; sigma2 = 77.99366; IC = 4.82744; PC = 72.60594; MSPE = 22.13889
#> r = 1; sigma2 = 13.65239; IC = 3.52566; PC = 21.67581; MSPE = 12.03686
#> r = 2; sigma2 = 8.56312; IC = 3.48518; PC = 19.23841; MSPE = 10.31254
#> *
#> r = 3; sigma2 = 6.40268; IC = 3.60547; PC = 18.61783; MSPE = 11.48390
#> r = 4; sigma2 = 4.74273; IC = 3.70145; PC = 16.93707; MSPE = 16.28613
#> r = 5; sigma2 = 4.02488; IC = 3.91847; PC = 17.05226; MSPE = 15.78683
#> 
#>  r* = 2
#> 
#> Bootstrapping for uncertainties ...
#> 1000 runs

3.5.4 Implied weights

out$wgt.implied (\(N_{co}\times N_{tr}\)) stores the implied weights of all control units for each treated unit. Different from the synthetic control method, the weights can take both positive and negative values. Below we show the control unit weights for Wisconsin.

dim(out_turnout$wgt.implied)
#> [1] 38  9
sort(out_turnout$wgt.implied[,8])
#>  [1] -0.420446734 -0.359404870 -0.358899140 -0.323621805 -0.275363471
#>  [6] -0.222140041 -0.214909889 -0.197804828 -0.185884567 -0.162290117
#> [11] -0.151519318 -0.148094608 -0.127000746 -0.064591440 -0.057043363
#> [16] -0.038932843 -0.001453018  0.010929464  0.029620626  0.049794411
#> [21]  0.073077120  0.079864605  0.090892631  0.091876103  0.093457125
#> [26]  0.104411283  0.133990028  0.158671615  0.159121640  0.181418421
#> [31]  0.182877791  0.221808796  0.226279566  0.250193486  0.278783695
#> [36]  0.280519519  0.295315162  0.316497707

3.5.5 Visualizing results

Like we have demonstrated with the multiperiod DID analysis, we also use the gap (default) plot to visualize the ATT.

plot(out_turnout, xlim = c(-10, 5), ylim=c(-15,15))

For staggered DID, a status plot can be generated after estimation. Here, we use xlab, ylab, and main to modify the axis labels and the graph title, respectively. Additionally, xangle and yangle can tilt the numeric labels to improve readability. Note that the values provided for these options specify the degree of tilt.

plot(out_turnout, type = "status",xlab = "Year", ylab = "State", main = "Treatment Status", 
     xticklabels=c(1920, 1928, 1936, 1944, 1952, 1960, 
                   1968, 1976, 1984, 1992, 2000, 2008), xangle=10)

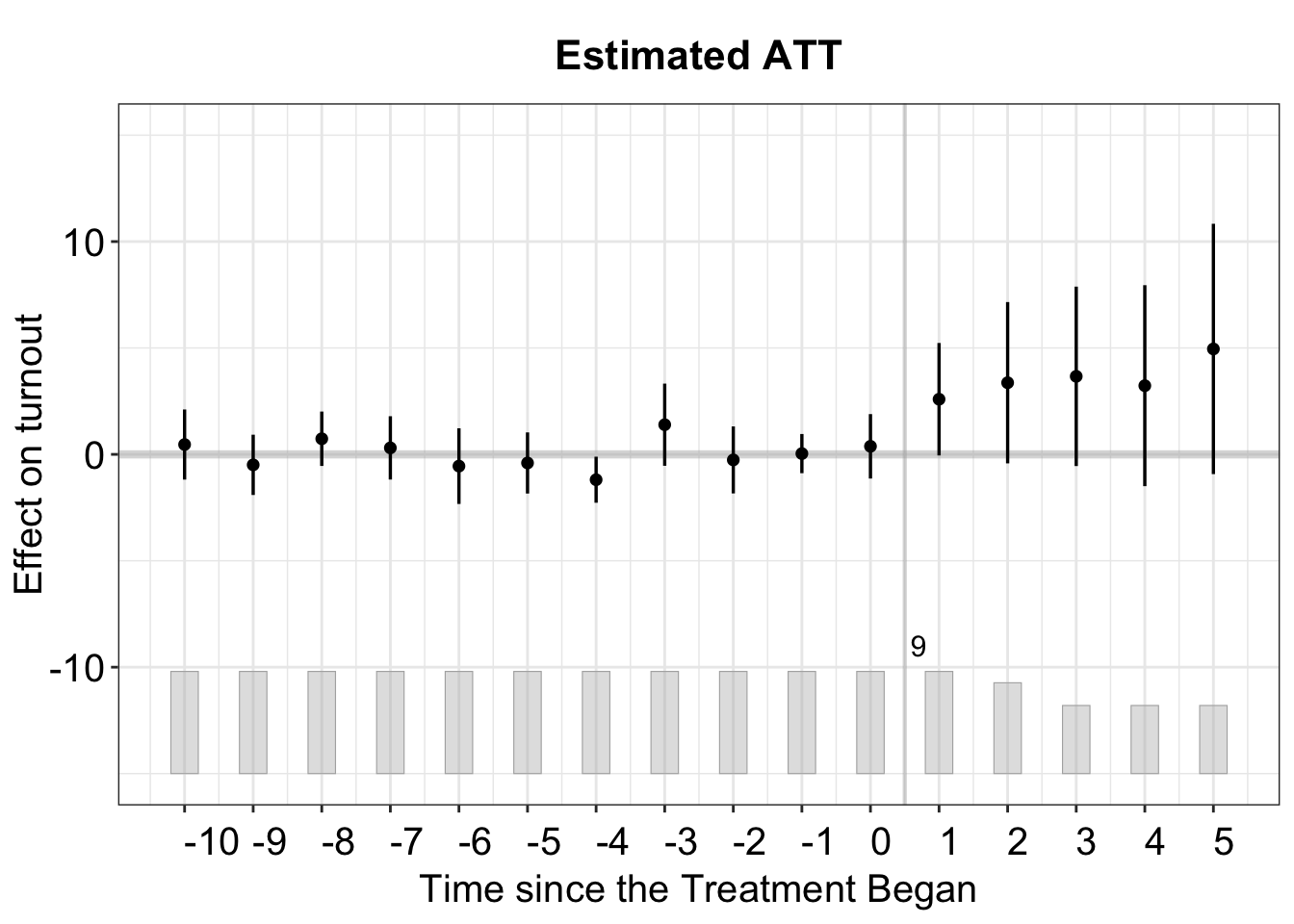
If we want to zoom in to examine the treatment effect on a specific state, such as Wisconsin, we can do so by setting the id option accordingly.

plot(out_turnout, type = "gap", id = "WI", main = "Wisconsin")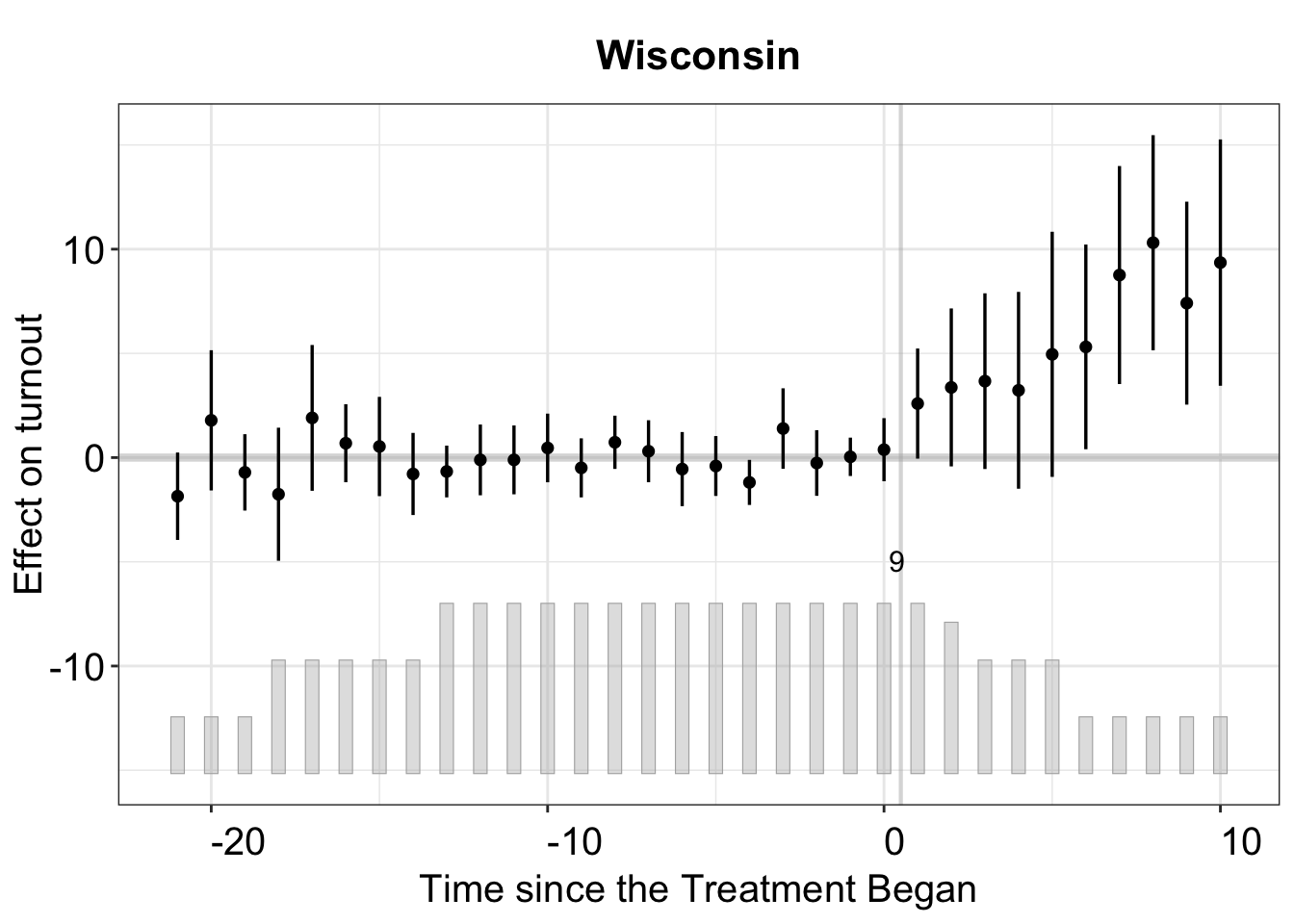

As we have seen in the last example, due to the small number of treated units, the box plot reduces to a scatter plot.

plot(out_turnout, type = "box", 
     xticklabels=c("-20", "-15", "-10", "-5","0","5","10"))

Here, we visualize the estimated average treatment effects by calendar time.

plot(out_turnout, type = "calendar", ylim = c(-15,15))

Estimated factors and factor loadings are ploted below.

plot(out_turnout, type = "factors", xlab = "Year")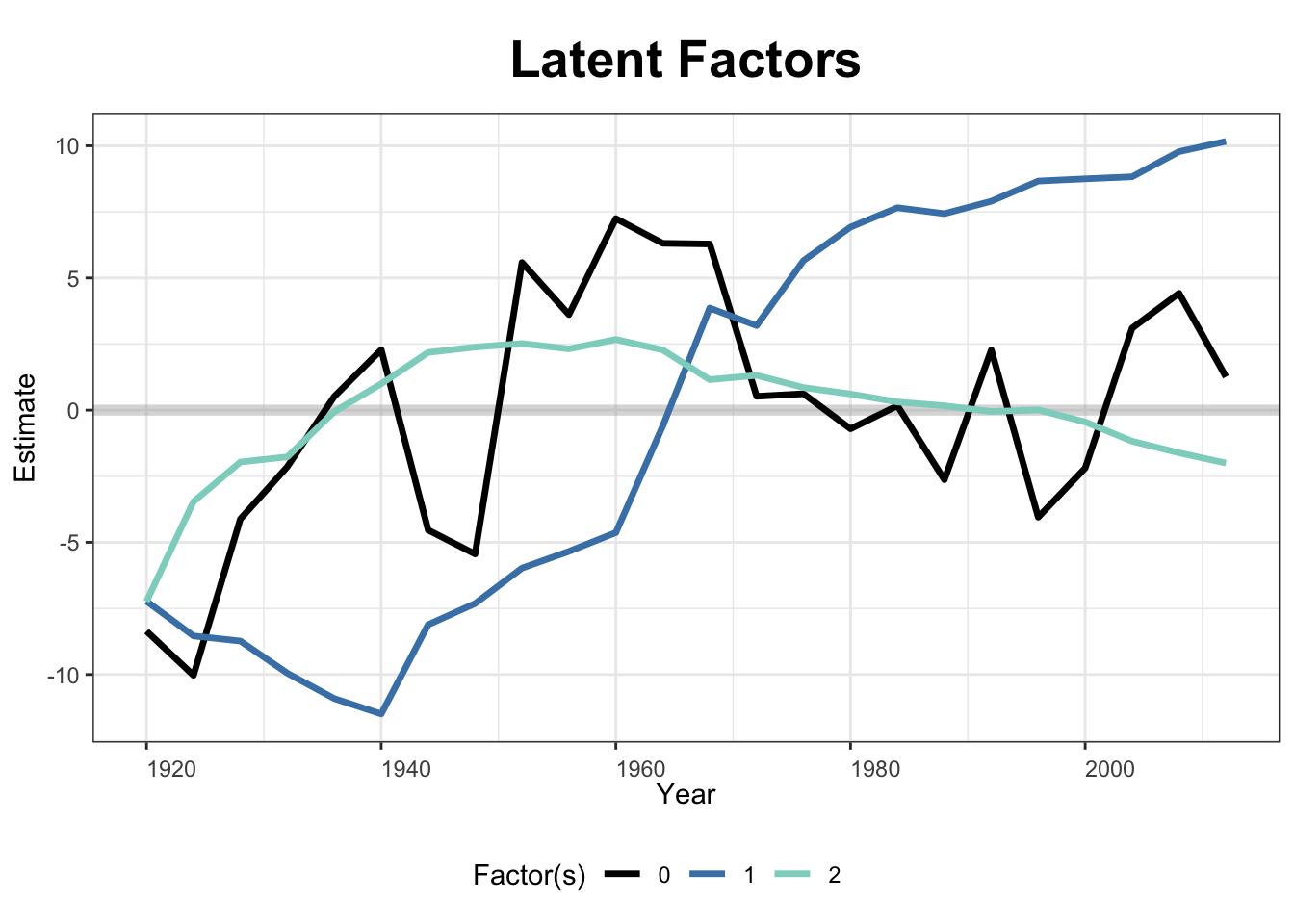

plot(out_turnout, type = "loadings")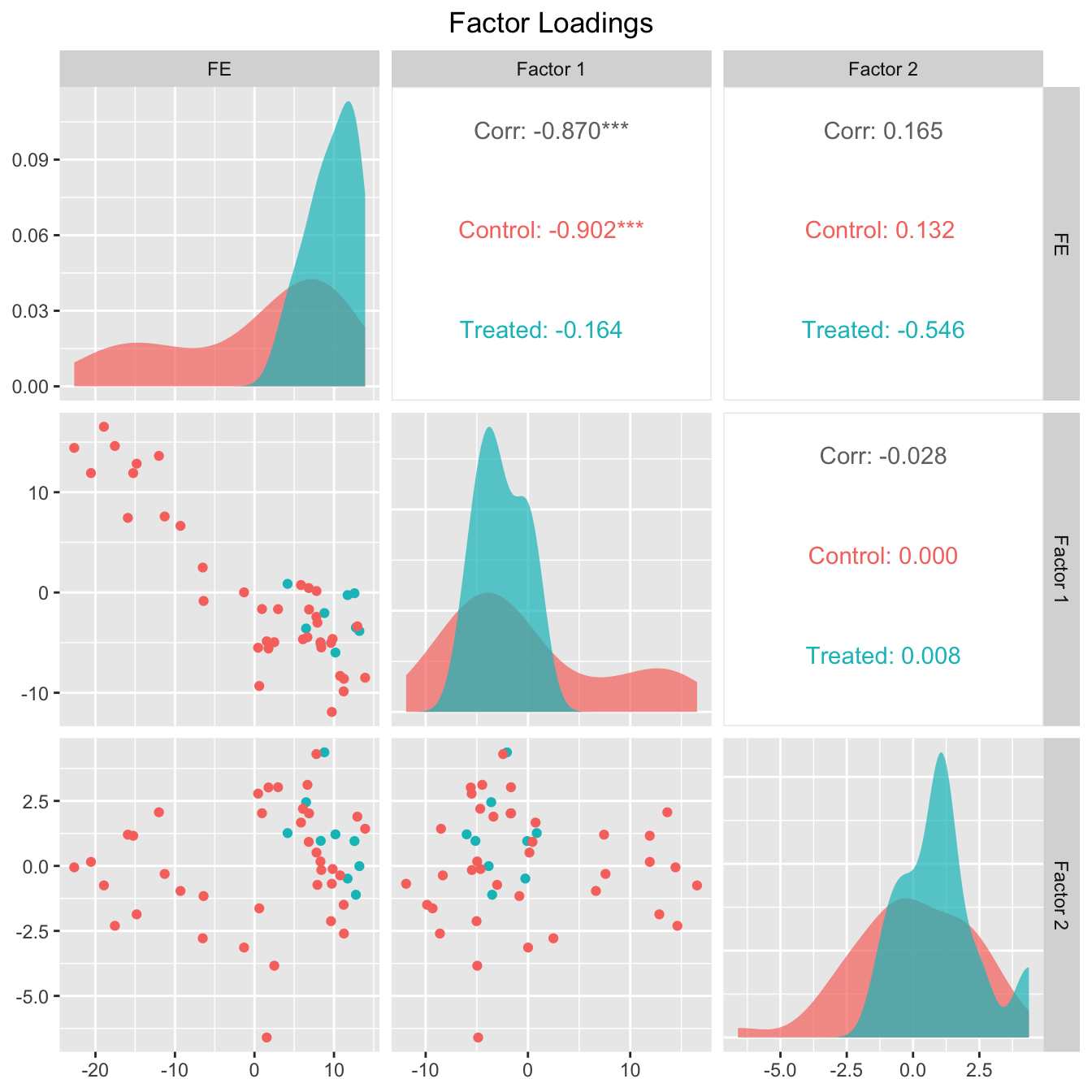

---

3.6 Unbalanced panels

Gsynth in fect can accommodate unbalanced panels. To illustrate how it works, we randomly remove 50 observations as well as the first 15 observations of Wyoming from the turnout dataset and then re-estimate the model.

set.seed(123456)
turnout.ub <- turnout[-c(which(turnout$abb=="WY")[1:15], 
                         sample(1:nrow(turnout),50,replace=FALSE)),]

Again, before running any regressions, we first plot the data structure and visualize missing values. In the following plot, white cells represent missing values.

panelview(turnout ~ policy_edr + policy_mail_in + policy_motor, 
          data = turnout.ub,  index = c("abb","year"), 
          pre.post = TRUE)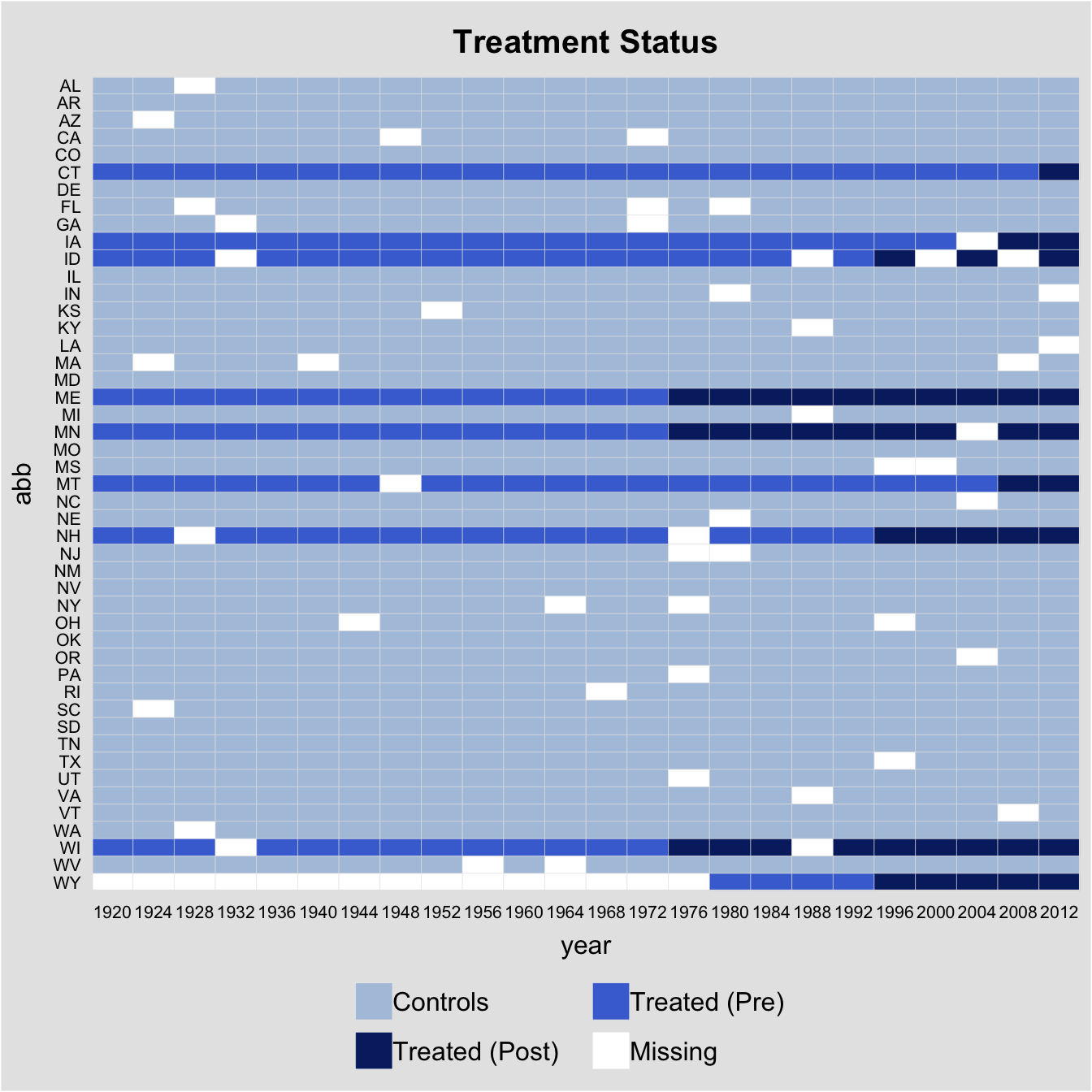 

3.6.1 Estimation

out_ub <- fect(turnout ~ policy_edr + policy_mail_in + policy_motor, 
              data = turnout.ub,  index = c("abb","year"), 
              se = TRUE, method = "gsynth", 
              r = c(0, 5), CV = TRUE, force = "two-way", 
              parallel = TRUE, min.T0 = 8, 
              nboots = 1000, seed = 02139)

3.6.2 Visualizing results

The status plot visualizes the regression data and differs from the panelView plot. Wyoming’s data is shown in gray, as its observations are excluded due to an insufficient number of pre-treatment periods.

The missing data matrix can also be accessed via out_ub$obs.missing, where values 0, 1, 2, 3, and 4 represent missing values, control observations, treated (pre-treatment) observations, treated (post-treatment) observations, and treated observations removed from the sample, respectively.

plot(out_ub, type = "status",
     xticklabels=c(1920, 1928, 1936, 1944, 1952, 1960, 
                   1968, 1976, 1984, 1992, 2000, 2008),
     xangle=10)

Like in panelView, we can plot specific observations by setting id and adjust labels on x-axis as needed.

plot(out_ub, type = "status", xlab = "Year", ylab = "State",
     main = "Treatment Status", id = out_ub$id[out_ub$tr],
     xlim = c(1920,2012), 
     xticklabels=c(1920, 1928, 1936, 1944, 1952, 1960,
                   1968, 1976, 1984, 1992, 2000, 2008))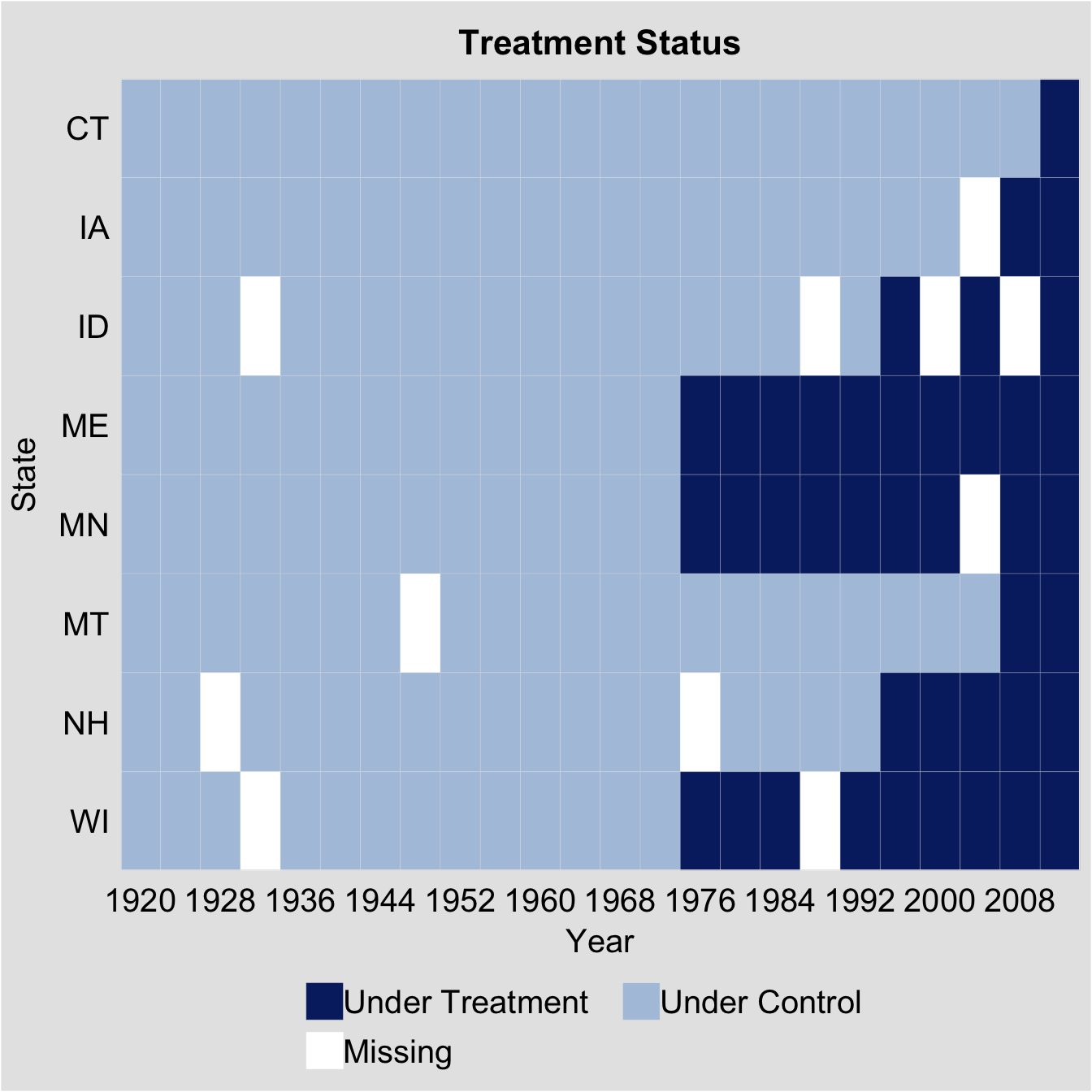

We re-produce the gap plot with the unbalanced panel, here, we set the range of y in between \((-10,20)\).

plot(out_ub, type = "gap", ylim = c(-10, 20))

3.6.3 Matrix completion

Finally, we re-estimate the model using the matrix completion method.

out.mc_ub <- fect(turnout ~ policy_edr + policy_mail_in + policy_motor, 
                 min.T0 = 8, data = turnout.ub,  
                 index = c("abb","year"), method = "mc", 
                 se = TRUE, nboots = 1000, seed = 02139)

Again, we use a gap plot to visualize estimated ATT.

plot(out.mc_ub, main = "Estimated ATT (MC)", ylim = c(-10, 20))

3.7 Additional Notes

1. Unbalanced Panels: Running Gsynth within fect on unbalanced panels will take significantly more time compared to balanced panels, often by a factor of 100:1 or more. This is because the EM algorithm, which fills in missing values (implemented in C++), requires many more iterations to converge. To reduce run-time, users can remove units or time periods with extensive missing values. Understanding the data structure before running any regressions is always helpful. Note that this approach differs from setting method = "ife", as no pre-treatment data from the treated units is used to impute \(\hat{Y}(0)\).

2. Adding Covariates: Including covariates in the model will significantly slow down the algorithm, as the IFE/MC model requires more time to converge. Users should be aware of this trade-off when incorporating covariates.

3. Setting min.T0: Setting min.T0 to a positive value helps. The algorithm will automatically exclude treated units with too few pre-treatment periods. A larger \(T_0\) reduces bias in causal estimates and minimizes the risk of severe extrapolation. When running cross-validation to select the number of factors, min.T0 must be equal to or greater than (r.max + 2). Errors frequently occur when there are too few pre-treatment periods, so ensuring adequate \(T_0\) (e.g. setting min.T0 = 5) is crucial.

Athey, Susan, Mohsen Bayati, Nikolay Doudchenko, Guido Imbens, and Khashayar Khosravi. 2021. “Matrix Completion Methods for Causal Panel Data Models.” Journal of the American Statistical Association 116 (536): 1716–30.

Borusyak, Kirill, Xavier Jaravel, and Jann Spiess. 2024. “Revisiting Event-Study Designs: Robust and Efficient Estimation.” Review of Economic Studies 91: 3253–85.

Gardner, John. 2021. “Two-Stage Differences in Differences.” Working Paper, Boston College. https://bit.ly/3AF32Af.

Gobillon, Laurent, and Thierry Magnac. 2016. “Regional Policy Evaluation: Interactive Fixed Effects and Synthetic Controls.” Review of Economics and Statistics 98 (3): 535–51.

Liu, Licheng, Ye Wang, and Yiqing Xu. 2024. “A Practical Guide to Counterfactual Estimators for Causal Inference with Time-Series Cross-Sectional Data.” American Journal of Political Science 68 (1): 160–76.

Sun, Liyang, and Sarah Abraham. 2021. “Estimating Dynamic Treatment Effects in Event Studies with Heterogeneous Treatment Effects.” Journal of Econometrics 225 (2): 175–99.

Xu, Yiqing. 2017. “Generalized Synthetic Control Method: Causal Inference with Interactive Fixed Effects Models.” Political Analysis 25 (1): 57–76.